题目内容
16．在拍毕业照时，六个同学排成一排照相，要求其中一对好友甲和乙相邻，且同学丙不能和甲相邻的概率为（ ）| A． | $\frac{1}{15}$ | B． | $\frac{2}{15}$ | C． | $\frac{4}{15}$ | D． | $\frac{1}{5}$ |
分析 根据题意，首先计算甲乙相邻时，五位同学站成一排的情况数目，用捆绑法，将甲与乙看成一个整体，计算可得其情况数目；再计算在此条件下，甲、丙相邻的情况数目，分析可得若甲、丙相邻，必须是甲、乙、丙三人相邻，且甲在中间，由捆绑法计算可得其情况数目；从而求出其中一对好友甲和乙相邻，且同学丙不能和甲相邻包含的基本事件个数，由等可能事件的概率公式，计算可得答案
解答 解：根据题意，六位同学站成一排合影留念，基本事件总数n=A${\;}_{6}^{6}$=720，
若甲乙相邻，将甲与乙看成一个整体，再与其他4人全排列，有A22×A55=240种情况，
若甲、丙相邻，必须是甲、乙、丙三人相邻，且甲在中间，
可先将甲、乙、丙三人看成一个整体，其中令甲在中间，再与其他3人全排列，有A22×A44=48种情况，
∴甲和乙相邻，且同学丙不能和甲相邻包含的基本事件个数m=240-48=192，
故甲和乙相邻，且同学丙不能和甲相邻的概率p=$\frac{m}{n}=\frac{192}{720}$=$\frac{4}{15}$．
故选：C．
点评 本题考查等可能事件的概率计算，涉及排列、组合的运用，考查推理论证能力、运算求解能力，考查化归与转化思想，是中档题．
练习册系列答案
相关题目
10．定义在实数域上的偶函数f（x）对于?x∈R，均满足条件f（x+2）=f（x）+f（1），且当x∈[2，3]时，f（x）=-2x2+12x-18，若函数y=f（x）-loga（|x|+1）在（0，+∞）上恰有4个零点，则a的值为（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{\sqrt{5}}{5}$ | D． | $\frac{\sqrt{6}}{6}$ |
与直线
间的距离是 ．
11．已知函数f（x）=$\left\{\begin{array}{l}x+\frac{2}{e}，x＜0\\ \frac{x}{e^x}，x≥0\end{array}$，若f（x1）=f（x2）=f（x3）（x1＜x2＜x3），则$\frac{{f（{x_2}）}}{x_1}$的取值范围是（ ）
| A． | （-1，0） | B． | （-2，-1） | C． | （-∞，0） | D． | （1，+∞） |
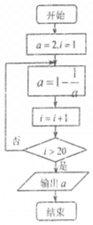
1．如果执行如图所示的程序框图，则输出的结果是（ ）
| A． | -4 | B． | -3 | C． | 2 | D． | 0 |
