题目内容
1.已知某圆的极坐标方程为ρ2-4$\sqrt{2}$ρcos(θ-$\frac{π}{4}$)+6=0,求:(1)圆的标准方程和参数方程;
(2)在圆上所有的点(x,y)中x•y的最大值和最小值.
分析 (1)ρ2-4$\sqrt{2}$ρcos(θ-$\frac{π}{4}$)+6=0,即ρ2-4$\sqrt{2}$×$\frac{\sqrt{2}}{2}$ρ(cosθ+sinθ)+6=0,利用互化公式可得直角坐标方程,再利用平方关系即可得出参数方程.
(2)设圆上的点$(2+\sqrt{2}cosθ,2+\sqrt{2}sinθ)$,则xy=4+2$\sqrt{2}$sinθ+2$\sqrt{2}$cosθ+2sinθcosθ,令sinθ+cosθ=$\sqrt{2}$sin$(θ+\frac{π}{4})$=t∈$[-\sqrt{2},\sqrt{2}]$,可得xy=4+2$\sqrt{2}$t+t2-1,即可得出.
解答 解:(1)ρ2-4$\sqrt{2}$ρcos(θ-$\frac{π}{4}$)+6=0,即ρ2-4$\sqrt{2}$×$\frac{\sqrt{2}}{2}$ρ(cosθ+sinθ)+6=0,
可得x2+y2-4x-4y+6=0,配方为:(x-2)2+(y-2)2=2.
可得参数方程:$\left\{\begin{array}{l}{x=2+\sqrt{2}cosθ}\\{y=2+\sqrt{2}sinθ}\end{array}\right.$(θ为参数).
(2)设圆上的点$(2+\sqrt{2}cosθ,2+\sqrt{2}sinθ)$,
则xy=4+2$\sqrt{2}$sinθ+2$\sqrt{2}$cosθ+2sinθcosθ,
令sinθ+cosθ=$\sqrt{2}$sin$(θ+\frac{π}{4})$=t∈$[-\sqrt{2},\sqrt{2}]$,
则t2=1+2sinθcosθ,可得sinθcosθ=$\frac{{t}^{2}-1}{2}$.
则xy=4+2$\sqrt{2}$t+t2-1=$(t+\sqrt{2})^{2}$+1∈[1,9].
∴xy的最大值最小值分别为1,9.
点评 本题考查了极坐标方程化为直角坐标方程、圆的参数方程及其应用,考查了推理能力与计算能力,属于中档题.

| A. | (-1,0) | B. | (-2,-1) | C. | (-∞,0) | D. | (1,+∞) |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $[{\frac{{2\sqrt{5}}}{5},2}]∪[{\frac{{6\sqrt{5}}}{5},6}]$ | B. | $[{\frac{{2\sqrt{5}}}{5},6}]$ | C. | $[{\frac{{2\sqrt{5}}}{5},2}]∪[{4,6}]$ | D. | $\left\{2\right\}∪[{\frac{{6\sqrt{5}}}{5},6}]$ |
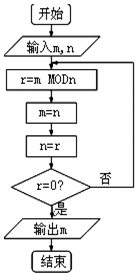 如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“mMODn”表示m除以n的余数),若输入的m,n分别为325,125,则输出的m=( )
如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“mMODn”表示m除以n的余数),若输入的m,n分别为325,125,则输出的m=( )