题目内容
已知函数f(x)=2sin
•cos
-2
cos2
+
(ω>0),其图象与直线y=2的相邻两个公共点之间的距离为2π.
(Ⅰ)若x∈[0,π],试求出函数f(x)的单调递减区间;
(Ⅱ)△ABC的三个内角A,B,C及其所对的边a,b,c满足条件:f(A)=0,a=2,且b,a,c成等比数列.试求
在
方向上的抽影n的值.
| ωx |
| 2 |
| ωx |
| 2 |
| 3 |
| ωx |
| 2 |
| 3 |
(Ⅰ)若x∈[0,π],试求出函数f(x)的单调递减区间;
(Ⅱ)△ABC的三个内角A,B,C及其所对的边a,b,c满足条件:f(A)=0,a=2,且b,a,c成等比数列.试求
| CA |
| CB |
考点:三角函数中的恒等变换应用,平面向量数量积的运算
专题:三角函数的图像与性质
分析:(Ⅰ)首先,根据二倍角公式,化简函数解析式,然后,根据周期公式,确定解析式,最后,结合三角函数的单调性进行求解;
(Ⅱ)首先,根据f(A)=0,得到A=
,结合余弦定理求解b=c,最后,求解结果.
(Ⅱ)首先,根据f(A)=0,得到A=
| π |
| 3 |
解答:
解:(Ⅰ)∵f(x)=2sin
•cos
-2
cos2
+
=sinωx-
cosωx
=2sin(ωx-
),
∴f(x)=2sin(ωx-
),
∵图象与直线y=2的相邻两个公共点之间的距离为2π.
∴T=
=2π,
∴ω=1,
∴f(x)=2sin(x-
),
∵x∈[0,π],
∴(x-
)∈[-
,
]
∵(x-
)∈[
,
,
∴x∈[
,π],
∴函数f(x)的单调递减区间[
,π].
(Ⅱ)根据(Ⅰ),得f(A)=2sin(A-
)=0,
∵A∈(0,π),
∴A=
,
∵b,a,c成等比数列.
∴a2=bc,
∵a2=b2+c2-2bccos
,
∴b=c,
∴B=C=
,
∴△ABC为等边三角形,
∴n=|
|cosC=1.
| ωx |
| 2 |
| ωx |
| 2 |
| 3 |
| ωx |
| 2 |
| 3 |
=sinωx-
| 3 |
=2sin(ωx-
| π |
| 3 |
∴f(x)=2sin(ωx-
| π |
| 3 |
∵图象与直线y=2的相邻两个公共点之间的距离为2π.
∴T=
| 2π |
| ω |
∴ω=1,
∴f(x)=2sin(x-
| π |
| 3 |
∵x∈[0,π],
∴(x-
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∵(x-
| π |
| 3 |
| π |
| 2 |
| 2π |
| 3 |
∴x∈[
| 5π |
| 6 |
∴函数f(x)的单调递减区间[
| 5π |
| 6 |
(Ⅱ)根据(Ⅰ),得f(A)=2sin(A-
| π |
| 3 |
∵A∈(0,π),
∴A=
| π |
| 3 |
∵b,a,c成等比数列.
∴a2=bc,
∵a2=b2+c2-2bccos
| π |
| 3 |
∴b=c,
∴B=C=
| π |
| 3 |
∴△ABC为等边三角形,
∴n=|
| CA |
点评:本题重点考查了三角函数的图象与性质、三角恒等变换公式、二倍角公式、解三角形和平面向量等知识,考查比较综合,属于中档题.

练习册系列答案
相关题目
 如图,点A是单位圆与x轴正半轴的交点,点B(-
如图,点A是单位圆与x轴正半轴的交点,点B(-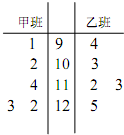 为了解甲、乙两个班级某次考试的数学成绩,从甲、乙两个班级中分别随机抽取5名学生的成绩(单位:分)作样本,如图是样本的茎叶图:
为了解甲、乙两个班级某次考试的数学成绩,从甲、乙两个班级中分别随机抽取5名学生的成绩(单位:分)作样本,如图是样本的茎叶图: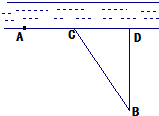 甲、乙两个工厂,甲厂位于一直线河岸的岸边A处,乙厂与甲厂在河的同侧,乙厂位于离河岸40千米的B处,乙厂到河岸的垂足D与A相距50千米,两厂要在此岸边AD之间合建一个供水站C,从供水站到甲厂和乙厂的水管费用分别为每千米3a元和5a元,若CD=x千米,设总的水管费用为y元,如图所示,
甲、乙两个工厂,甲厂位于一直线河岸的岸边A处,乙厂与甲厂在河的同侧,乙厂位于离河岸40千米的B处,乙厂到河岸的垂足D与A相距50千米,两厂要在此岸边AD之间合建一个供水站C,从供水站到甲厂和乙厂的水管费用分别为每千米3a元和5a元,若CD=x千米,设总的水管费用为y元,如图所示,