题目内容

已知函数f（x）=2cos2x+2sinxsin（x+
π
2
），
（Ⅰ）求函数f（x）的最小正周期；
（Ⅱ）求函数f（x）在区间[0，
π
2
]上的值域．
考点：三角函数中的恒等变换应用,三角函数的周期性及其求法
专题：三角函数的图像与性质
分析：（Ⅰ）首先，根据二倍角公式化简函数解析式：f（x）=
2
sin（2x+
π
4
）+1，然后，根据周期公式进行求解；
（Ⅱ）根据x∈[0，
π
2
]，从而确定
π
4
≤2x+
π
4
≤
5π
4
，然后，根据三角函数的图象与性质进行求解．
解答： 解：（1）∵f（x）=2cos2x+2sinxcosx
=cos2x+sin2x+1
=
2
sin（2x+
π
4
）+1，
∴f（x）=
2
sin（2x+
π
4
）+1，
∴T=
2π
2
=π
∴f（x）的最小正周期π，
（2）∵x∈[0，
π
2
]，
∴
π
4
≤2x+
π
4
≤
5π
4
，
∴-
2
2
≤sin（2x+
π
4
）≤1，
∴0≤f（x）≤1+
2
，
∴函数在区间[0，
π
2
]上的值域为[0，1+
2
]．
点评：本题综合考查了二倍角公式、周期公式、三角函数的单调性等知识，属于中档题．
练习册系列答案
相关题目
设f（x）=ex（ax2-7x+13），其中a∈R，曲线y=f（x）在点（1，f（1））处的切线与直线l：2ex-y+e=0平行．
（1）确定a的值；
（2）求函数f（x）的单调区间．
已知函数f（x）=（mx+n）e-x（m，n∈R，e为自然数）
①若函数f（x）在点（1，f（1））处的切线方程为x+ey-3=0，试确定函数f（x）的单调区间．
②当n=-1，m∈R时，若对于任意x∈[
1
2
，1]都有f（x）≥x恒成立，求实数m的最小值．
如图，△ABC的三个内角分别为A，B，C，cosA=
1
3
，cosB=
2
2
3
．CD是∠ACB的角平分线．
（1）求角C的大小；
（2）当CD=8
2
-4，求AC，BC的长．
已知函数f（x）=2sin
ωx
2
•cos
ωx
2
-2
3
cos2
ωx
2
+
3
（ω＞0），其图象与直线y=2的相邻两个公共点之间的距离为2π．
（Ⅰ）若x∈[0，π]，试求出函数f（x）的单调递减区间；
（Ⅱ）△ABC的三个内角A，B，C及其所对的边a，b，c满足条件：f（A）=0，a=2，且b，a，c成等比数列．试求
CA
在
CB
方向上的抽影n的值．
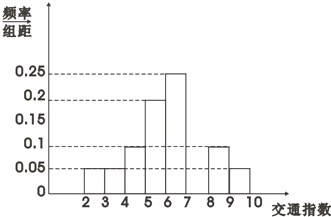交通指数是交通拥堵指数的简称，是综合反映道路网畅通或拥堵的概念，记交通指数为T．其范围为[0，10]，分别有五个级别：T∈[0，2）畅通；T∈[2，4）基本畅通； T∈[4，6）轻度拥堵； T∈[6，8）中度拥堵；T∈[8，10]严重拥堵，晚高峰时段（T≥2），从某市交通指挥中心选取了市区20个交通路段，依据其交通指数数据绘制的部分直方图如图所示．
（Ⅰ）请补全直方图，并求出轻度拥堵、中度拥堵、严重拥堵路段各有多少个？
（Ⅱ）用分层抽样的方法从交通指数在[4，6），[6，8），[8，l0]的路段中共抽取6个路段，求依次抽取的三个级别路段的个数；
（Ⅲ）从（Ⅱ）中抽出的6个路段中任取2个，求至少一个路段为轻度拥堵的概率．
曲线y=x3+x2-1在点P（-1，-1）处的切线方程是
 
．
设函数y=f（x）的定义域为R，若存在常数M＞0，使|f（x）|≤M|x|对一切实数x均成立，则称为“有界泛函”．现在给出如下5个函数：
①f（x）=x2；   
②f(x)=
x
x2+x+1
；  
③f（x）=sinx；  
④y=xcosx；
⑤f（x）是R上的奇函数，且满足对一切x1，x2∈R，均有|f（x1）-f（x2）|≤|x1-x2|．
其中属于“有界泛函”的函数是
 
（填上所有正确的序号）
设f（x）是定义在R上的偶函数，当x＜0时，f′（x）＞0，且f（-2）=0，则不等式f（x）＜0的解集为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网