题目内容
已知sin(α+
)=
,sin(α-
)=
,求sinα,cosα和tanα的值.
| π |
| 4 |
| 3 |
| 5 |
| π |
| 4 |
| 4 |
| 5 |
考点:两角和与差的正弦函数,同角三角函数基本关系的运用
专题:计算题,三角函数的求值
分析:由两角和与差的正弦函数化简,经计算可得sinα,cosα和tanα的值.
解答:
解:sin(α+
)=
⇒sinα
+cosα
=
;
sin(α-
)=
⇒sinα
-cosα
=
;
两式相加,有:sinα=
.
两式相减,有:cosα=-
.
故:tanα=-7.
| π |
| 4 |
| 3 |
| 5 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 5 |
sin(α-
| π |
| 4 |
| 4 |
| 5 |
| ||
| 2 |
| ||
| 2 |
| 4 |
| 5 |
两式相加,有:sinα=
7
| ||
| 10 |
两式相减,有:cosα=-
| ||
| 10 |
故:tanα=-7.
点评:本题主要考察两角和与差的正弦函数和同角三角函数基本关系的运用,属于基础题.

练习册系列答案
相关题目
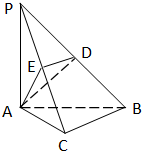 如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D、E分别是棱PB、PC的中点.
如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D、E分别是棱PB、PC的中点.