题目内容
设等差数列{an}的前n项和为Sn，若a6+a9＞0，S15＜0，则Sn取得最大值时n为（ ）
| A、6 | B、7 | C、8 | D、9 |
考点：等差数列的前n项和
专题：等差数列与等比数列
分析：由已知条件得a6+a9=a7+a8＞0，S15=15a8＜0，从a8开始为负，当n=7时S7最大．
解答：
解：{an}为等差数列
a6+a9=a7+a8＞0，
S15=
（a1+a15）
=15a8＜0，
∴a7＞0
从a8开始为负，
∴当n=7时S7最大．
故选：B．
a6+a9=a7+a8＞0，
S15=
| 15 |
| 2 |
=15a8＜0，
∴a7＞0
从a8开始为负，
∴当n=7时S7最大．
故选：B．
点评：本题考查Sn取得最大值时n的求法，是中档题，解题时要注意等差数列的性质的灵活运用．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
某班有4个空位，安排从外校转来的3个学生坐到这4个空位上，每人一个座位，则不同的坐法有（ ）
| A、24种 |
| B、43种 |
| C、34种 |
| D、4种 |
定义
为n个正数x1，x2，…，xn的“平均倒数”．若正项数列{an}的前n项的“平均倒数”为
，则数列{an}的通项公式为an=（ ）
| n |
| x1+x2+…xn |
| 1 |
| 3n+2 |
| A、3n+2 |
| B、6n-1 |
| C、（3n-1）（3n+2） |
| D、4n+1 |
曲线y=x2+2与直线5x-y+2=0所围成的图形面积是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
设实数a，b，c满足a+b+c=0，则a，b，c中（ ）
| A、至多有一个不大于0 |
| B、至少有一个不小于0 |
| C、至多有两个不小于0 |
| D、至少有两个不小于0 |
计算∫
cosxdx=（ ）
0 |
| A、-1 | ||
| B、1 | ||
C、
| ||
| D、0 |
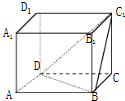如图长方体ABCD-A1B1C1D1中，AB=AD=2
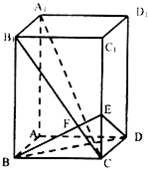已知长方体AC1中，棱AB=BC=1，棱BB1=2，连结B1C，过B点作B1C的垂线交CC1于E，交B1C于F．