题目内容
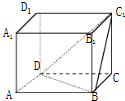 如图长方体ABCD-A1B1C1D1中,AB=AD=2
如图长方体ABCD-A1B1C1D1中,AB=AD=2| 3 |
| 2 |
(1)求BC1与面ACC1A1所成角的大小;
(2)求二面角C1-BD-C的大小.
考点:二面角的平面角及求法,直线与平面所成的角
专题:空间角
分析:(1)根据线面角的定义即可求BC1与面ACC1A1所成角的大小;
(2)根据二面角的定义,求出二面角的平面角,根据三角形的边角关系,即可求二面角C1-BD-C的大小.
(2)根据二面角的定义,求出二面角的平面角,根据三角形的边角关系,即可求二面角C1-BD-C的大小.
解答:
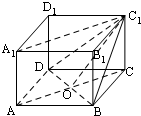 解:(1)∵AB=AD=2
解:(1)∵AB=AD=2
,
∴底面ABCD是正方形,连结AC交BD于O,
则BD⊥AC,
则BD⊥面ACC1A1,
则∠BC1O是BC1与面ACC1A1所成的角,
∵AB=AD=2
,CC1=
.
∴AC=2
,OC=OB=
,BC1=
,
则sin∠BC1O=
=
=
.
则∠BC1O=arcsin
.
即BC1与面ACC1A1所成角的大小为arcsin
.
(2)∵AB=AD=2
,CC1=
.
∴DC1=BC1=
,
则△DC1B是等腰三角形,则OC1⊥BD,
即∠C1OC为二面角C1-BD-C的平面角,
则tan∠C1OC=
=
=
,
即∠C1OC=
,
即二面角C1-BD-C的大小为
.
 解:(1)∵AB=AD=2
解:(1)∵AB=AD=2| 3 |
∴底面ABCD是正方形,连结AC交BD于O,
则BD⊥AC,
则BD⊥面ACC1A1,
则∠BC1O是BC1与面ACC1A1所成的角,
∵AB=AD=2
| 3 |
| 2 |
∴AC=2
| 6 |
| 6 |
| 14 |
则sin∠BC1O=
| OB |
| BC1 |
| ||
|
| ||
| 7 |
则∠BC1O=arcsin
| ||
| 7 |
即BC1与面ACC1A1所成角的大小为arcsin
| ||
| 7 |
(2)∵AB=AD=2
| 3 |
| 2 |
∴DC1=BC1=
| 14 |
则△DC1B是等腰三角形,则OC1⊥BD,
即∠C1OC为二面角C1-BD-C的平面角,
则tan∠C1OC=
| CC1 |
| OC |
| ||
|
| ||
| 3 |
即∠C1OC=
| π |
| 6 |
即二面角C1-BD-C的大小为
| π |
| 6 |
点评:本题主要考查直线和平面所成的角以及二面角的大小,根据定义求出相应的平面角是解决本题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
如果椭圆
+
=1上一点P到焦点F1的距离为6,则点P到另一个焦点F2的距离为( )
| x2 |
| 100 |
| y2 |
| 36 |
| A、10 | B、6 | C、12 | D、14 |
设等差数列{an}的前n项和为Sn,若a6+a9>0,S15<0,则Sn取得最大值时n为( )
| A、6 | B、7 | C、8 | D、9 |
过点(0,3)且与直线y=-4x+1平行的直线方程为( )
| A、4x+y-3=0 |
| B、4x+y+3=0 |
| C、4x-y+3=0 |
| D、4x-y-3=0 |
新定义运算
=ad-bc,函数f(x)=
,下列命题正确的是( )
|
|
| A、函数f(x)是周期为π的偶函数 | ||
| B、函数f(x)是周期为2π的偶函数 | ||
C、函数f(x)是向右平移
| ||
D、函数f(x)是向左平移
|