题目内容
 已知变量x,y满足
已知变量x,y满足
|
(1)画出不等式组表示的平面区域.
(2)设z=3x+y,求z的最大值及相应点的坐标.
考点:简单线性规划
专题:不等式的解法及应用
分析:(1)由不等式的意义可得不等式组表示平面区域;(2)变形目标函数y=-3x+z,平移直线y=-3x,由截距的意义可得.
解答:
 解:(1)不等式组表示平面区域如阴影部分所示:
解:(1)不等式组表示平面区域如阴影部分所示:
(2)∵z=3x+y,∴y=-3x+z
z为斜率为-3的直线的纵截距,
如图作直线y=-3x,平移该直线,
当平移到经过该阴影部分的P点时,纵截距z最大,
联立
,解得点P (2,1),
∴此时z=3x+y取得最大值是7
 解:(1)不等式组表示平面区域如阴影部分所示:
解:(1)不等式组表示平面区域如阴影部分所示:(2)∵z=3x+y,∴y=-3x+z
z为斜率为-3的直线的纵截距,
如图作直线y=-3x,平移该直线,
当平移到经过该阴影部分的P点时,纵截距z最大,
联立
|
∴此时z=3x+y取得最大值是7
点评:本题考查简单线性规划,准确作图是解决问题的关键,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
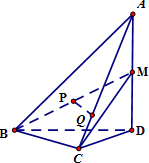 如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,CD=2,AD=4.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,CD=2,AD=4.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC. 如图,在斜三棱柱ABC-A1B1C1中,O是AC的中点,A1O⊥平面ABC,∠BCA=90°,AA1=AC=BC.
如图,在斜三棱柱ABC-A1B1C1中,O是AC的中点,A1O⊥平面ABC,∠BCA=90°,AA1=AC=BC. 如图,在正方体ABCD-A1B1C1D1中,E、F分别为AD1,CD1中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别为AD1,CD1中点.