题目内容
已知函数f(x)=
(a∈R)
(1)作出a=
时函数f(x)的图象;
(2)若函数f(x)在R上单调递减,求a的取值范围.
|
(1)作出a=
| 1 |
| 2 |
(2)若函数f(x)在R上单调递减,求a的取值范围.
考点:分段函数的应用
专题:函数的性质及应用
分析:(1)a=
时函数f(x)=
,作出直线y=
x+2后取x<1的部分;再作出对数函数y=log
x的图象,取x≥1的部分.
(2)若函数f(x)在R上单调递减,则当x≥1时函数y=logax递减,故0<a<1,同时函数y=(3a-1)x+4a递减,需满足3a-1<0且函数值≥0.
| 1 |
| 2 |
|
| 1 |
| 2 |
| 1 |
| 2 |
(2)若函数f(x)在R上单调递减,则当x≥1时函数y=logax递减,故0<a<1,同时函数y=(3a-1)x+4a递减,需满足3a-1<0且函数值≥0.
解答:
解:(1)a=
时函数f(x)=
,画此分段函数如图:
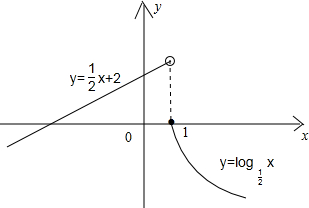
(2)要使函数f(x)在R上单调递减,则当x≥1时函数y=logax递减,∴0<a<1,
同时函数y=g(x)=(3a-1)x+4a递减且g(1)≥0,即
,∴
≤a<
,
∴a的取值范围:{a|
≤a<
}.
| 1 |
| 2 |
|

(2)要使函数f(x)在R上单调递减,则当x≥1时函数y=logax递减,∴0<a<1,
同时函数y=g(x)=(3a-1)x+4a递减且g(1)≥0,即
|
| 1 |
| 7 |
| 1 |
| 3 |
∴a的取值范围:{a|
| 1 |
| 7 |
| 1 |
| 3 |
点评:本题考查分段函数图象的作法,涉及函数的单调性,属中档题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
设全集U=R,集合A={x|x≥1},B={x|0≤x<5},则集合(∁UA)∩B=( )
| A、{x|0<x<1} |
| B、{x|0<x≤1} |
| C、{x|0≤x<1} |
| D、{x|0≤x≤1} |
已知数列{an}满足a1=2,an+1=
,则a2014等于( )
| 1+an |
| 1-an |
| A、2 | ||
| B、-3 | ||
C、-
| ||
D、
|
若sina•
-cosa•
=-1,且a≠
﹙k∈z﹚,则a所在的象限是( )
| (sin2a) |
| (cos2a) |
| kπ |
| 2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
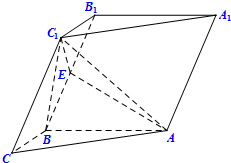 如图,在三棱柱ABC-A1B1C1中,已知AB⊥BB1C1C,BC=1,AB=BB1=2,∠BCC1=
如图,在三棱柱ABC-A1B1C1中,已知AB⊥BB1C1C,BC=1,AB=BB1=2,∠BCC1=