题目内容
20．设f（x）是定义在R上的奇函数，当x＜0时，f（x）=2x+1，则f（0）+f（1）=（ ）| A． | $-\frac{3}{2}$ | B． | 1 | C． | $\frac{1}{2}$ | D． | 5 |
分析 根据函数奇偶性的性质将条件进行转化求解即可．
解答 解：∵f（x）是定义在R上的奇函数，当x＜0时，f（x）=2x+1，
∴f（0）=0，
f（1）=-f（-1）=-（$\frac{1}{2}$+1）=$-\frac{3}{2}$，
则f（0）+f（1）=$-\frac{3}{2}$，
故选：A
点评 本题主要考查函数值的计算，根据函数奇偶性的性质进行转化求解是解决本题的关键．
练习册系列答案
智慧小复习系列答案
相关题目
10．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F1，F2，点P满足|PF1|-|PF2|=2a，若$\overrightarrow{PM}$+$\overrightarrow{{F}_{1}M}$=$\overrightarrow{0}$，且M（0，b），则双曲线C的渐近线方程为（ ）
| A． | y=±2x | B． | y=±$\sqrt{5}$x | C． | y=±2$\sqrt{2}$x | D． | y=±$\sqrt{3}$x |
8．
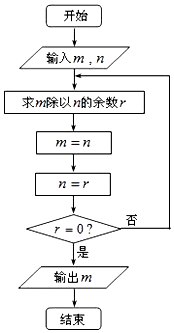如图所示的程序框图描述的算法称为“欧几里得”辗转相除法，若输入m=2821，n=2015，则输出的m的值为（ ）
如图所示的程序框图描述的算法称为“欧几里得”辗转相除法，若输入m=2821，n=2015，则输出的m的值为（ ）| A． | 1 | B． | 403 | C． | 806 | D． | 2015 |
5．
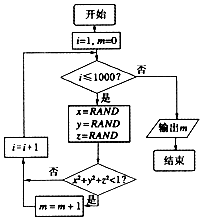我们可以用随机模拟的方法估计π的值，如图程序框图表示其基本步骤（函数RAND是产生随机数的函数，它能随机产生（0，1）内的任何一个实数）．若输出的结果为527，则由此可估计π的近似值为（ ）
我们可以用随机模拟的方法估计π的值，如图程序框图表示其基本步骤（函数RAND是产生随机数的函数，它能随机产生（0，1）内的任何一个实数）．若输出的结果为527，则由此可估计π的近似值为（ ）| A． | 3.126 | B． | 3.132 | C． | 3.151 | D． | 3.162 |
12．已知ω为正整数，函数f（x）=sinωxcosωx+${cos^2}ωx-\frac{1}{2}$在区间$（{-\frac{π}{3}，\frac{π}{12}}）$内单调递增，则函数f（x）（ ）
| A． | 最小值为$-\frac{1}{2}$，其图象关于点$（{\frac{π}{4}，0}）$对称 | |
| B． | 最大值为$\frac{{\sqrt{2}}}{2}$，其图象关于直线$x=-\frac{π}{8}$对称 | |
| C． | 最小正周期为2π，其图象关于点$（{\frac{3π}{4}，0}）$对称 | |
| D． | 最小正周期为π，其图象关于直线$x=-\frac{3π}{8}$对称 |