题目内容
若
=2,则2sinθcosθ= .
| sinθ+cosθ |
| sinθ-cosθ |
考点:同角三角函数基本关系的运用
专题:计算题,三角函数的求值
分析:先求出tanθ=3,再利用2sinθcosθ=
=
,代入即可得出结论.
| 2sinθcosθ |
| sin2θ+cos2θ |
| 2tanθ |
| tan2θ+1 |
解答:
解:∵
=2,
∴tanθ=3,
∴2sinθcosθ=
=
=
,
故答案为:
| sinθ+cosθ |
| sinθ-cosθ |
∴tanθ=3,
∴2sinθcosθ=
| 2sinθcosθ |
| sin2θ+cos2θ |
| 2tanθ |
| tan2θ+1 |
| 3 |
| 5 |
故答案为:
| 3 |
| 5 |
点评:本题考查同角三角函数基本关系的运用,考查学生计算能力,利用2sinθcosθ=
=
是关键.
| 2sinθcosθ |
| sin2θ+cos2θ |
| 2tanθ |
| tan2θ+1 |

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
 在如图所示的“茎叶图”表示的数据中,众数和中位数分别( )
在如图所示的“茎叶图”表示的数据中,众数和中位数分别( )| A、23与26 |
| B、31与24 |
| C、24与30 |
| D、26与30 |
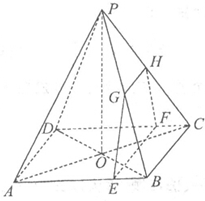 如图,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为2
如图,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为2