题目内容
已知圆x2+y2=4内一点A(1,1),P,Q为圆上的动点,若PA⊥QA,求PQ中点M的轨迹方程.
考点:轨迹方程
专题:计算题,作图题,坐标系和参数方程
分析:作出图象辅助,由题意设P(2cosa,2sina),Q(2cosθ,2sinθ),则M=(x,y)=(cosa+cosθ,sina+sinθ),由PA⊥QA可得
•
=0,化简可得轨迹方程.
| AP |
| AQ |
解答:
 解:如右图,
解:如右图,
设P(2cosa,2sina),Q(2cosθ,2sinθ),
则M=(x,y)=(cosa+cosθ,sina+sinθ),
∵PA⊥QA,
∴
•
=0,
∴(2cosa-1,2sina-1)•(2cosθ-1,2sinθ-1)=0,
∴(2cosa-1)(2cosθ-1)+(2sina-1)(2sinθ-1)=0,
∴4cosacosθ)-2(cosa+cosθ)+1+4sinasinθ-2(sina+sinθ)+1=0①,
又∵(cosa+cosθ)2+(sina+sinθ)2=2+2(cosacosθ+sinasinθ),
∴4(cosacosθ+sinasinθ)=2[(cosa+cosθ)2+(sina+sinθ)2-2],
则①式可化为
2[(cosa+cosθ)2+(sina+sinθ)2-2]-2(cosa+cosθ)+1-2(sina+sinθ)+1=0,
即2(x2+y2-2)-2x+1-2y+1=0,
即x2+y2-x-y-1=0.
 解:如右图,
解:如右图,设P(2cosa,2sina),Q(2cosθ,2sinθ),
则M=(x,y)=(cosa+cosθ,sina+sinθ),
∵PA⊥QA,
∴
| AP |
| AQ |
∴(2cosa-1,2sina-1)•(2cosθ-1,2sinθ-1)=0,
∴(2cosa-1)(2cosθ-1)+(2sina-1)(2sinθ-1)=0,
∴4cosacosθ)-2(cosa+cosθ)+1+4sinasinθ-2(sina+sinθ)+1=0①,
又∵(cosa+cosθ)2+(sina+sinθ)2=2+2(cosacosθ+sinasinθ),
∴4(cosacosθ+sinasinθ)=2[(cosa+cosθ)2+(sina+sinθ)2-2],
则①式可化为
2[(cosa+cosθ)2+(sina+sinθ)2-2]-2(cosa+cosθ)+1-2(sina+sinθ)+1=0,
即2(x2+y2-2)-2x+1-2y+1=0,
即x2+y2-x-y-1=0.
点评:本题考查了参数方程及轨迹方程的求法,属于中档题.

练习册系列答案
相关题目
 将底边BC长为6
将底边BC长为6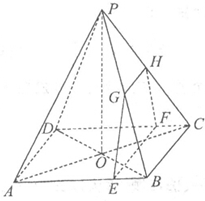 如图,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为2
如图,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为2