题目内容
已知数列{an}的前n项和为Sn,且满足a1=2,nan+1=Sn+n(n+1).
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)设Tn为数列{
}的前n项和,求Tn;
(Ⅲ)设bn=
,证明:b1+b2+b3+…+bn<
.
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)设Tn为数列{
| an |
| 2n |
(Ⅲ)设bn=
| 1 |
| anan+1an+2 |
| 1 |
| 32 |
考点:数列的求和,数列递推式
专题:点列、递归数列与数学归纳法
分析:(Ⅰ)由a1=2,nan+1=Sn+n(n+1),可以推出an+1-an=2(n≥2),易证a2=a1+2,从而可知数列{an}为以2为首项,2为公差的等差数列,继而可求数列{an}的通项公式an;
(Ⅱ)由(Ⅰ)得
=
=
,利用错位相减法即可求得数列{
}的前n项和Tn;
(Ⅲ)由(Ⅰ)知,bn=
=
[
-
],从而可证b1+b2+b3+…+b<
.
(Ⅱ)由(Ⅰ)得
| an |
| 2n |
| 2n |
| 2n |
| n |
| 2n-1 |
| an |
| 2n |
(Ⅲ)由(Ⅰ)知,bn=
| 1 |
| 2n•2(n+1)•2(n+2) |
| 1 |
| 16 |
| 1 |
| n(n+1) |
| 1 |
| (n+1)(n+2) |
| 1 |
| 32 |
解答:
(Ⅰ)解:由n∈N*时,nan+1=Sn+n(n+1)①
得n≥2时,(n-1)an=Sn-1+(n-1)n②
①-②,得nan+1-(n-1)an=an+2n,即an+1-an=2(n≥2)…2分
又当n=1时,a2=S1+1×2,
所以,a2=a1+2,…3分
所以对一切正整数n,有an+1-an=2,所以数列{an}为以2为首项,2为公差的等差数列,故an=2n…4分
(Ⅱ)解:由(Ⅰ)得
=
=
,…5分
所以Tn=1+
+
+…+
,①
两边同乘以
,得
Tn=
+
+
+…+
+
,②
①-②,得
Tn=1+
+
+…+
-
,
整理得T=4-
…8分
(Ⅲ)证明:由(Ⅰ)知,bn=
=
[
-
]…9分
所以,b1+b2+b3+…+bn=
(
-
+
-
+…+
-
)
=
(
-
)=
-
<
…13分
得n≥2时,(n-1)an=Sn-1+(n-1)n②
①-②,得nan+1-(n-1)an=an+2n,即an+1-an=2(n≥2)…2分
又当n=1时,a2=S1+1×2,
所以,a2=a1+2,…3分
所以对一切正整数n,有an+1-an=2,所以数列{an}为以2为首项,2为公差的等差数列,故an=2n…4分
(Ⅱ)解:由(Ⅰ)得
| an |
| 2n |
| 2n |
| 2n |
| n |
| 2n-1 |
所以Tn=1+
| 2 |
| 2 |
| 3 |
| 22 |
| n |
| 2n-1 |
两边同乘以
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 22 |
| 3 |
| 23 |
| n-1 |
| 2n-1 |
| n |
| 2n |
①-②,得
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
| n |
| 2n |
整理得T=4-
| n+2 |
| 2n+1 |
(Ⅲ)证明:由(Ⅰ)知,bn=
| 1 |
| 2n•2(n+1)•2(n+2) |
| 1 |
| 16 |
| 1 |
| n(n+1) |
| 1 |
| (n+1)(n+2) |
所以,b1+b2+b3+…+bn=
| 1 |
| 16 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n(n+1) |
| 1 |
| (n+1)(n+2) |
=
| 1 |
| 16 |
| 1 |
| 2 |
| 1 |
| (n+1)(n+2) |
| 1 |
| 32 |
| 1 |
| 16(n+1)(n+2) |
| 1 |
| 32 |
点评:本题考查数列递推式及数列求和,着重考查错位相减法与裂项法的应用,考查综合运算与推理论证能力,属于难题.

练习册系列答案
相关题目
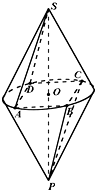 如图两个共底面的相同的圆锥,底面圆心为O,顶点分别为S和P,四边形ABCD是圆O的内接矩形,连接SA,SD,PC,PB
如图两个共底面的相同的圆锥,底面圆心为O,顶点分别为S和P,四边形ABCD是圆O的内接矩形,连接SA,SD,PC,PB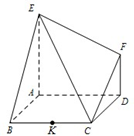 如图,已知多面体EABCDF的底面ABCD是边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=
如图,已知多面体EABCDF的底面ABCD是边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=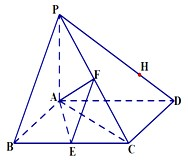 四棱锥P-ABCD底面是菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
四棱锥P-ABCD底面是菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.