题目内容
已知函数f(x)=
(x>0).
(1)试判断函数f(x)在(0,+∞)上单调性并证明你的结论;
(2)若f(x)>
恒成立,求整数k的最大值;
(3)求证:22×33×44×55×…×nn×(n+1)n+1>e n2.
| 1+ln(x+1) |
| x |
(1)试判断函数f(x)在(0,+∞)上单调性并证明你的结论;
(2)若f(x)>
| k |
| x+1 |
(3)求证:22×33×44×55×…×nn×(n+1)n+1>e n2.
考点:利用导数研究函数的单调性,导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(1)通过求导得f′(x)<0,从而问题解决,
(2)f(x)>
恒成立,即h(x)=
>k即h(x)的最小值大于k.而h′(x)=
,记g(x)=x-1-ln(x+1),(x>0),g(x)=0存在唯一实根a,且满足a∈(2,3),a=1+ln(a+1),从而解决问题,
(3)由(2)知
>
,(x>0),化简可得ln(x+1)x+1>2x-1,相加得:ln22+ln33+…+ln(n+1)n+1>2×1-1+2×2-1+…+2n-1,即 ln22+ln33+…+ln(n+1)n+1>n2,从而问题证出.
(2)f(x)>
| k |
| x+1 |
| (x+1)[1+ln(x+1)] |
| x |
| x-1-ln(x+1) |
| x2 |
(3)由(2)知
| 1+ln(x+1) |
| x |
| 3 |
| x+1 |
解答:
解:(1)f′(x)=-
[
+ln(x+1)],
∵x>0,∴x2>0,
>0,ln(x+1)>0,
∴f′(x)<0,
∴f(x)在(0,+∞)上是减函数.
(2)f(x)>
恒成立,即h(x)=
>k即h(x)的最小值大于k.
而h′(x)=
,记g(x)=x-1-ln(x+1),(x>0),
则g′(x)=
>0,∴g(x)在(0,+∞)上单调递增,
又g(2)=1-ln3<0,g(3)=2-2ln2>0,
∴g(x)=0存在唯一实根a,且满足a∈(2,3),a=1+ln(a+1),
当x>a时,g(x)>0,h′(x)>0,
当0<x<a时,g(x)<0,h′(x)<0,
∴h(x)min=h(a)=
=a+1∈(3,4),
故正整数k的最大值是3,
(3)由(2)知
>
,(x>0),
化简可得ln(x+1)x+1>2x-1,
∴ln22>2×1-1,ln33>2×2-1,…,ln(n+1)n+1>2n-1,
相加得:ln22+ln33+…+ln(n+1)n+1>2×1-1+2×2-1+…+2n-1,
即 ln22+ln33+…+ln(n+1)n+1>n2,
∴22×33×44×55×…×nn×(n+1)n+1>e n2.
| 1 |
| x2 |
| 1 |
| x+1 |
∵x>0,∴x2>0,
| 1 |
| x+1 |
∴f′(x)<0,
∴f(x)在(0,+∞)上是减函数.
(2)f(x)>
| k |
| x+1 |
| (x+1)[1+ln(x+1)] |
| x |
而h′(x)=
| x-1-ln(x+1) |
| x2 |
则g′(x)=
| x |
| x+1 |
又g(2)=1-ln3<0,g(3)=2-2ln2>0,
∴g(x)=0存在唯一实根a,且满足a∈(2,3),a=1+ln(a+1),
当x>a时,g(x)>0,h′(x)>0,
当0<x<a时,g(x)<0,h′(x)<0,
∴h(x)min=h(a)=
| (a+1)[1+ln(a+1)] |
| a |
故正整数k的最大值是3,
(3)由(2)知
| 1+ln(x+1) |
| x |
| 3 |
| x+1 |
化简可得ln(x+1)x+1>2x-1,
∴ln22>2×1-1,ln33>2×2-1,…,ln(n+1)n+1>2n-1,
相加得:ln22+ln33+…+ln(n+1)n+1>2×1-1+2×2-1+…+2n-1,
即 ln22+ln33+…+ln(n+1)n+1>n2,
∴22×33×44×55×…×nn×(n+1)n+1>e n2.
点评:本题考察了函数的单调性,函数的最值,不等式的证明,导数的应用,是一道综合题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目

 如图,已知正方体ABCD-A1B1C1D1的棱长为2,M为正方形AA1D1D的中心,N为棱AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,M为正方形AA1D1D的中心,N为棱AB的中点. 如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.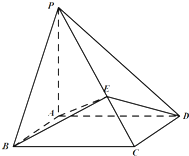 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,BC=
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,BC=