题目内容
cos70°•cos20°-sn70°•sin20°的值是（ ）
| A、0 | B、1 |
| C、sin50° | D、cos50° |
考点：两角和与差的正弦函数
专题：三角函数的求值
分析：利用两角和的余弦函数公式化简后即可得答案．
解答：
解：cos70°•cos20°-sn70°•sin20°=cos（70°+20°）=cos90°=0，
故选：A．
故选：A．
点评：本题主要考查了两角和与差的余弦函数公式的应用，属于基础题．
练习册系列答案
相关题目
若tan（2π+α）=-
，则
的值是（ ）
| 1 |
| 2 |
| 2sinαcosα |
| sin2α-cos2α |
A、
| ||
| B、3 | ||
C、-
| ||
| D、-3 |
类比三角形中的性质：
（1）两边之和大于第三边；
（2）中位线长等于底边的一半；
（3）三内角平分线交于一点；
可得四面体的对应性质：
（1）任意三个面的面积之和大于第四个面的面积；
（2）过四面体的交于同一顶点的三条棱的中点的平面面积等于第四个面面积的
；
（3）四面体的六个二面角的平分面交于一点．
其中类比推理结论正确的有（ ）
（1）两边之和大于第三边；
（2）中位线长等于底边的一半；
（3）三内角平分线交于一点；
可得四面体的对应性质：
（1）任意三个面的面积之和大于第四个面的面积；
（2）过四面体的交于同一顶点的三条棱的中点的平面面积等于第四个面面积的
| 1 |
| 4 |
（3）四面体的六个二面角的平分面交于一点．
其中类比推理结论正确的有（ ）
| A、（1） |
| B、（1）（2） |
| C、（1）（2）（3） |
| D、都不对 |
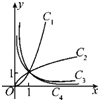图中的曲线是幂函数y=xn在第一象限的图象，已知n可取±2，±| 1 |
| 2 |
A、-2，-
| ||||
B、2，
| ||||
C、-
| ||||
D、2，
|
直线
x+y-2
=0的倾斜角为（ ）
| 3 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
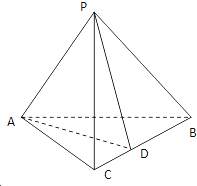如图，在三棱锥P-ABC中，AC=BC=2，∠ACB=90°，AP=BP=AB，PC⊥AC，点D为BC中点．
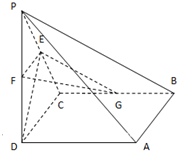如图所示，在四棱锥P-ABCD中，底面ABCD为正方形，PD⊥平面ABCD，PD=AB=2，E、F分别为PC、PD的中点．