题目内容
已知复数
=1-i，则复数z的共轭复数
等于（ ）
| 2 |
| z |
. |
| z |
| A、-2i | B、2i |
| C、1-i | D、1+i |
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：利用复数的运算法则、共轭复数的定义即可得出．
解答：
解：∵复数
=1-i，∴z=
=
=1+i，
则复数z的共轭复数
=1-i．
故选：C．
| 2 |
| z |
| 2 |
| 1-i |
| 2(1+i) |
| (1-i)(1+i) |
则复数z的共轭复数
. |
| z |
故选：C．
点评：本题考查了复数的运算法则、共轭复数的定义，属于基础题．
练习册系列答案
相关题目
已知
=2-i，则在复平面内，复数z对应的点位于（ ）
| ||
| 1-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
sin47°cos17°-cos47°sin17°=（ ）
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
若tan（2π+α）=-
，则
的值是（ ）
| 1 |
| 2 |
| 2sinαcosα |
| sin2α-cos2α |
A、
| ||
| B、3 | ||
C、-
| ||
| D、-3 |
已知tanαsinα＜0且sinαcosα＞0，则α所在象限为（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
圆心为（1，-1），半径为5的圆的标准方程为（ ）
| A、（x-1）2+（y+1）2=5 |
| B、（x+1）2+（y-1）2=5 |
| C、（x-1）2+（y+1）2=25 |
| D、（x+1）2+（y-1）2=25 |
下列各组函数表示相等函数的是（ ）
A、y=
| |||
B、y=
| |||
| C、y=x0与 y=1 | |||
D、y=
|
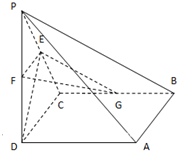如图所示，在四棱锥P-ABCD中，底面ABCD为正方形，PD⊥平面ABCD，PD=AB=2，E、F分别为PC、PD的中点．