题目内容
8.已知直线l:x-y=1与圆M:x2+y2-2x+2y=0相交于A,C两点,点B,D分别在圆M上运动,且位于直线AC两侧,则四边形ABCD面积的最大值为2$\sqrt{3}$.分析 先求出弦长|AB|的长度,然后结合圆与直线的位置关系图象,然后将ABCD的面积看成两个三角形△ABC和△ACD的面积之和,分析可得当BD为AC的垂直平分线时,四边形ABCD的面积最大.
解答 解:把圆Γ:x2+y2-2x+2y-1=0化为标准方程:(x-1)2+(y+1)2=2,圆心(1,-1),半径r=$\sqrt{2}$.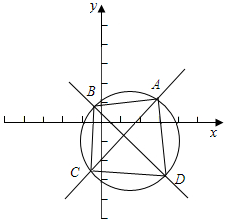
直线与圆相交,由点到直线的距离公式的弦心距d=$\frac{\sqrt{2}}{2}$.
由勾股定理的弦长|AB|=2$\sqrt{{r}^{2}-{d}^{2}}$=$\frac{\sqrt{6}}{2}$×$2=\sqrt{6}$,
又B,D两点在圆上,并且位于直线l的两侧,
四边形ABCD的面积可以看成是两个三角形△ABC和△ACD的面积之和,
如图所示,当B,D为如图所示位置,即BD为弦AC的垂直平分线时(即为直径时),
两三角形的面积之和最大,即四边形ABCD的面积最大,
最大面积为:S=$\frac{1}{2}$×|AB|×|CE|+$\frac{1}{2}$×|AB|×|DE|=$\frac{1}{2}$|AB|•|CD|=$\frac{1}{2}×\sqrt{6}×2\sqrt{2}$=2$\sqrt{3}$,
故答案为:2$\sqrt{3}$.
点评 本题涉及到圆与位置关系的题目,可采用数形结合思想,实现代数和几何间的转化,然后分析题目具体问题,求解即可,属于中档题

练习册系列答案
相关题目
18.已知m,n为空间中两条不同的直线,α,β为空间中两个不同的平面,下列命题正确的是( )
| A. | 若n⊥α,n⊥β,m?β则m∥α | B. | 若m⊥α,α⊥β,则m∥β | ||
| C. | 若m,n在γ内的射影互相平行,则m∥n | D. | 若m⊥l,α∩β=l,则m⊥α |
19.命题p:“?x0∈R,x02-x0>0”,则¬p是( )
| A. | ?x0∈R,x02-x0<0 | B. | ?x0∈R,x02-x0≤0 | C. | ?x∈R,x2-x<0 | D. | ?x∈R,x2-x≤0 |
3.已知离心率为$\frac{{2\sqrt{3}}}{3}$的双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右焦点为F,若线段OF的垂直平分线与双曲线一条渐近线的交点到另一条渐近线的距离为λc(c为半焦距,λ>0),则实数λ的值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | 2 | D. | 3 |
20.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左焦点为F,第二象限的点M在双曲线C的渐近线上,且|OM|=a,若直线|MF|的斜率为$\frac{b}{a}$,则双曲线C的渐近线方程为( )
| A. | y=±x | B. | y=±2x | C. | y=±3x | D. | y=±4x |
17.已知z∈C,i是虚数单位,$\overline{z}$是z的共轭复数,则下列说法与“z为纯虚数”不等价的是( )
| A. | z2<0 | B. | $z+\overline{z}=0$ | ||
| C. | Rez=0且 Imz≠0 | D. | z=|z|i或z=-|z|i,且|z|≠0 |
18.已知一个三角形内有2016个点,且任意一个点都不在其他任何两点的连线上,则这些点(含三角形三个顶点)将该三角形分成互相没有重合部分的三角形区域有( )
| A. | 4033个 | B. | 4032个 | C. | 2017个 | D. | 2016个 |