题目内容
已知函数f(x)=
，下列叙述
（1）f（x）是奇函数；
（2）y=xf（x）是奇函数；
（3）（x+1）f（x）-4＜0的解为-3＜x＜1
（4）xf（x+1）＜0的解为-1＜x＜1；其中正确的是 （填序号）．
|
（1）f（x）是奇函数；
（2）y=xf（x）是奇函数；
（3）（x+1）f（x）-4＜0的解为-3＜x＜1
（4）xf（x+1）＜0的解为-1＜x＜1；其中正确的是
考点：命题的真假判断与应用,函数单调性的性质,函数奇偶性的判断
专题：函数的性质及应用,不等式的解法及应用,简易逻辑
分析：由题中的函数解析式和奇函数的定义分别去判断①的正误；利用奇函数与奇函数的乘积是偶函数判断②的正误；根据分段函数对x分三种情况，求解对应的不等式得解集，最后再并在一起，判断③④的正误．
解答：
解：函数f(x)=
，
对于（1），由题意知f（0）=0且函数的定义域是R，当x＞0时，f（-x）=-2=-f（x），
当x＜0时，f（-x）=-2=-f（x），故（1）正确；
对于（2），由（1）可知f（x）是奇函数，y=x也是奇函数，∴y=xf（x）是偶函数不是奇函数，故（2）不正确；
对于（3），当x=0时，f（0）=0＜4，成立；当x＞0时，（x+1）f（x）-4＜0不等式为x+1＜2解得0＜x＜1；
当x＜0时，不等式为-x-1＜2，解得-3＜x＜0；
综上，不等式得解集是（-3，1），故（3）正确；
对于（4），当x=-1时，f（-1+1）=0＜0，不等式无解；
当x＞-1时，x+1＞0，不等式xf（x+1）＜0化为2x＜0解得x＜0，不等式的解为：-1＜x＜0；
当x＜-1时，不等式为-2x＜0，解得x＞0，不等式无解；
综上，不等式得解集解集为{x|-1＜x＜0}，故（4）不正确；
故答案为：（1）（3）．
|
对于（1），由题意知f（0）=0且函数的定义域是R，当x＞0时，f（-x）=-2=-f（x），
当x＜0时，f（-x）=-2=-f（x），故（1）正确；
对于（2），由（1）可知f（x）是奇函数，y=x也是奇函数，∴y=xf（x）是偶函数不是奇函数，故（2）不正确；
对于（3），当x=0时，f（0）=0＜4，成立；当x＞0时，（x+1）f（x）-4＜0不等式为x+1＜2解得0＜x＜1；
当x＜0时，不等式为-x-1＜2，解得-3＜x＜0；
综上，不等式得解集是（-3，1），故（3）正确；
对于（4），当x=-1时，f（-1+1）=0＜0，不等式无解；
当x＞-1时，x+1＞0，不等式xf（x+1）＜0化为2x＜0解得x＜0，不等式的解为：-1＜x＜0；
当x＜-1时，不等式为-2x＜0，解得x＞0，不等式无解；
综上，不等式得解集解集为{x|-1＜x＜0}，故（4）不正确；
故答案为：（1）（3）．
点评：本题的考查是分段函数判断奇偶性和求分段函数构成的不等式的解集，需要根据分段函数的不同范围对应不同的解析式进行对x分类进行求解．
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
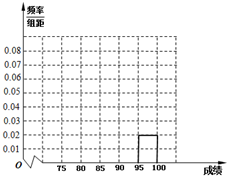某高中毕业学年，在高校自主招生期间，把学生的平时成绩按“百分制”折算，排出前n名学生，并对这n名学生按成绩分组，第一组[75，80），第二组[80，85），第三组[85，90），第四组[90，95），第五组[95，100]，如图为频率分布直方图的一部分，其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列，且第四组的人数为60．
已知函数f（x）的定义域为[-1，5]，部分对应值如下表，f（x）的导函数y=f′（x）的图象如图所示，给出关于f（x）的下列命题：