题目内容
14．
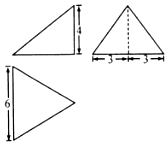如图，某三棱锥的正视图、侧视图和俯视图分别是直角三角形、等腰三角形和等边三角形，若该三棱锥的顶点都在同一球面上，则该球的表面积为（ ）| A． | 27π | B． | 48π | C． | 64π | D． | 81π |
分析 作出几何体的直观图，确定外接球的球心位置，利用勾股定理求出外接球半径即可得出表面积．
解答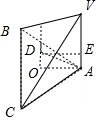 
解：由三视图可知该几何体为三棱锥，棱锥的高VA=4，棱锥底面ABC是边长为6的等边三角形，
作出直观图如图所示：
∵△ABC是边长为6的等边三角形，∴外接球的球心D在底面ABC的投影为△ABC的中心O，
过D作DE⊥VA于E，则E为VA的中点，
连结OA，DA，则DE=OA=$\frac{2}{3}×3\sqrt{3}$=2$\sqrt{3}$，AE=$\frac{1}{2}$VA=2，DA为外接球的半径r，
∴r=$\sqrt{D{E}^{2}+A{E}^{2}}$=4，
∴外接球的表面积S=4πr2=64π．
故选C．
点评 本题考查了棱锥的三视图，棱锥与外接圆的位置关系，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
4．设i是虚数单位，若复数$\frac{a-i}{1+2i}$为纯虚数，则实数a的值是（ ）
| A． | $-\frac{1}{2}$ | B． | 0 | C． | $\frac{1}{2}$ | D． | 2 |
9．下列符号判断正确的是（ ）
| A． | sin4＞0 | B． | cos（-3）＞0 | C． | tan4＞0 | D． | tan（-3）＜0 |
19．已知向量$\overrightarrow m，\overrightarrow n$分别是直线l的方向向量和平面α的法向量，若$cos\left?{\overrightarrow m，\left.{\overrightarrow n}\right＞}\right.=-\frac{1}{2}$，则l与α所成的角为（ ）
| A． | 150° | B． | 120° | C． | 60° | D． | 30° |
6．已知某几何体的三视图如图所示，则该几何体的表面积为 （ ）
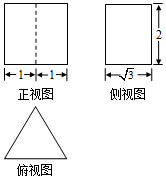
| A． | 12 | B． | 8+2$\sqrt{3}$ | C． | 12+2$\sqrt{3}$ | D． | 12+4$\sqrt{3}$ |
3．为了对某班学生的数学、物理成绩进行分析，从该班25位男同学，15位女同学中随机抽取一个容量为8的样本．
（1）如果按性别比例分层抽样，可以得到多少个不同的样本？（只要求写出算式，不必计算出结果）；
（2）若这8人的数学成绩从小到大排序是65，68，72，79，81，88，92，95．物理成绩从小到大排序是72，77，80，84，86，90，93，98．
①求这8人中恰有3人数学、物理成绩均在85分以上的概率（结果用分数表示）；
②已知随机抽取的8人的数学成绩和物理成绩如表：
若以数学成绩为解释变量x，物理成绩为预报变量y，求y关于x的线性回归方程（系数精确到0.01）；并求数学成绩对于物理成绩的贡献率R2（精确到0.01）．
参考公式：相关系数：r=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sqrt{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}\sum_{i=1}^{n}（{y}_{i}-\overline{y}）^{2}}}$，R2=r2，
回归方程：$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$，其$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$
参考数据：$\overline{x}$=80，$\overline{y}$=85，$\sum_{i=1}^{8}$（xi-$\overline{x}$）2=868，$\sum_{i=1}^{8}$（yi-$\overline{y}$）2═518，$\sum_{i=1}^{8}$（xi-$\overline{x}$）（yi-$\overline{y}$）=664，$\sqrt{868}$≈29.5，$\sqrt{518}$≈22.8．
（1）如果按性别比例分层抽样，可以得到多少个不同的样本？（只要求写出算式，不必计算出结果）；
（2）若这8人的数学成绩从小到大排序是65，68，72，79，81，88，92，95．物理成绩从小到大排序是72，77，80，84，86，90，93，98．
①求这8人中恰有3人数学、物理成绩均在85分以上的概率（结果用分数表示）；
②已知随机抽取的8人的数学成绩和物理成绩如表：
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学成绩 | 65 | 68 | 72 | 79 | 81 | 88 | 92 | 95 |
| 物理成绩 | 72 | 77 | 80 | 84 | 86 | 90 | 93 | 98 |
参考公式：相关系数：r=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sqrt{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}\sum_{i=1}^{n}（{y}_{i}-\overline{y}）^{2}}}$，R2=r2，
回归方程：$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$，其$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$
参考数据：$\overline{x}$=80，$\overline{y}$=85，$\sum_{i=1}^{8}$（xi-$\overline{x}$）2=868，$\sum_{i=1}^{8}$（yi-$\overline{y}$）2═518，$\sum_{i=1}^{8}$（xi-$\overline{x}$）（yi-$\overline{y}$）=664，$\sqrt{868}$≈29.5，$\sqrt{518}$≈22.8．
4．如图是某个几何体的三视图，则该几何体的体积是（ ）
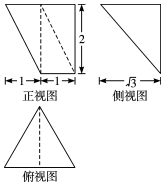
| A． | $\sqrt{3}$ | B． | 2 | C． | 3 | D． | 4 |