已知某几何体的三视图如图所示.则该几何体的表面积为 ( )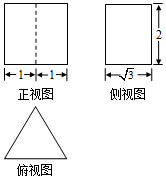 A．12B．8+2$\sqrt{3}$C．12+2$\sqrt{3}$D．12+4$\sqrt{3}$ 题目和参考答案——青夏教育精英家教网—

题目内容

6．已知某几何体的三视图如图所示，则该几何体的表面积为（　　）

A．

B．

8+2$\sqrt{3}$

C．

12+2$\sqrt{3}$

D．

12+4$\sqrt{3}$

分析根据题意，分析可得原几何体为三棱柱，且三棱柱的上下底面为边长为2的正三角形，其高为2，计算其表面积即可得答案．

解答解：根据题意，由三视图分析可得，原几何体为三棱柱，
其上下底面为边长为2的正三角形，其高为2，
则其表面积S=2×（$\frac{1}{2}$×2×$\sqrt{3}$）+（2+2+2）×2=12+2$\sqrt{3}$，
故选：C．

点评本题考查由三视图计算几何体的表面积，关键是分析还原几何体．

练习册系列答案

相关题目

16．

如图所示，某中学兴趣小组设计的自动小车按下面程序运行：
①由点A出发到达点B或C或D，到达点B，C，D之一就停止；
②每次只向右或向下按路线运行；
③在每个路口向下的概率为$\frac{1}{3}$；
④到达点P时只向下，到达点Q时只向右；
（1）求小车从点A出发经过点M到达点B的概率以及小车从点A出发经过点N到达点C的概率；
（2）若小车到达点B，C，D时，随机变量X分别记为1，2，3，求X的分布列及数学期望．

17．

如图，三棱锥O-ABC中，AO⊥平面OBC，且OA=OB=OC=2，∠BOC=60°，点E，F分别是AB，AC的中点，H为EF的中点，过EF的动平面与线段OA交于点A₁，与线段OB，OC的延长线分别相交于点B₁，C₁．
（Ⅰ）证明：B₁C₁⊥平面OAH；
（Ⅱ）当|BB₁|=2|OA₁|-2时，求二面角A-A₁E-F的正弦值．

14．

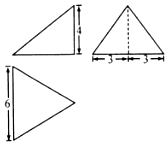如图，某三棱锥的正视图、侧视图和俯视图分别是直角三角形、等腰三角形和等边三角形，若该三棱锥的顶点都在同一球面上，则该球的表面积为（　　）

1．已知实数x，y满足约束条件$\left\{{\begin{array}{l}{2x-y+1≥0}\\{x≤1}\\{x-y≤0}\end{array}}\right.$则z=3x-2y的最小值是-3．

11．已经cos（2θ-3π）=$\frac{7}{25}$，且θ是第四象限角，
（1）求cosθ和sinθ的值；
（2）求$\frac{{cos（\frac{π}{2}-θ）}}{tanθ[cos（π+θ）-1]}$+$\frac{{sin（θ-\frac{3π}{2}）}}{tan（π-θ）cos（-θ）}$的值．

18．扇形AOB的中心角为2θ，θ∈（0，$\frac{π}{2}$），半径为r，在扇形AOB中作内切圆O₁与圆O₁外切，与OA，OB相切的圆O₂，问sinθ为何值时，圆O₂的面积最大？最大值是多少？

15．已知偶函数f（x）是定义在{x∈R|x≠0}上的可导函数，其导函数为f'（x）．当x＜0时，$f'（x）＜\frac{f（x）}{x}$恒成立．设m＞1，记$a=\frac{4mf（m+1）}{m+1}$，$b=2\sqrt{m}f（2\sqrt{m}）$，$c=（m+1）f（\frac{4m}{m+1}）$，则a，b，c的大小关系为（　　）

16．已知球O的表面积为25π，长方体的八个顶点都在球O的球面上，则这个长方体的表面积的最大值为（　　）

试题分类