题目内容
13.已知数列{an}满足an>1,过点(an,0)的直线ln与圆x2+y2=1在第一象限相切于点Pn,若记Pn的横坐标为bn,则$\frac{{a}_{1}{b}_{1}+{a}_{2}{b}_{2}+..+{a}_{n}{b}_{n}}{({a}_{1}{a}_{2}…{a}_{n})({b}_{1}{b}_{2}…{b}_{n})}$等于( )| A. | 2-21-n | B. | 2n-1 | C. | 1 | D. | n |
分析 设点Pn(bn,cn),即有bn2+cn2=1,即有切线的斜率,再由两直线垂直的条件,可得anbn=1,n∈N*,代入所求式子,即可得到所求值.
解答 解:设点Pn(bn,cn),即有bn2+cn2=1,
则切线的斜率为kn=$\frac{{c}_{n}}{{b}_{n}-{a}_{n}}$,
由OPn⊥ln,可得$\frac{{c}_{n}}{{b}_{n}-{a}_{n}}$•$\frac{{c}_{n}}{{b}_{n}}$=-1,
可得anbn=1,n∈N*,
则$\frac{{a}_{1}{b}_{1}+{a}_{2}{b}_{2}+..+{a}_{n}{b}_{n}}{({a}_{1}{a}_{2}…{a}_{n})({b}_{1}{b}_{2}…{b}_{n})}$=$\frac{1+1+…+1}{({a}_{1}{b}_{1})({a}_{2}{b}_{2})…({a}_{n}{b}_{n})}$=n.
故选:D.
点评 本题考查直线和圆相切的条件,考查两直线垂直的条件:斜率之积为-1,考查运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.某种型号的书包原价为a元,如果连续两次以相同的百分率x降价,那么两次降价后价格为多少元?( )
| A. | a(1-x) | B. | a(1-x)2 | C. | a(1-2x) | D. | 以上都不是 |
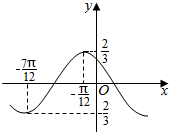 函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)图象的一段如图所示
函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)图象的一段如图所示