题目内容
1.若两点A(0,a)、B(0,b)(a>b>0),点P在x轴正半轴上运动,试求当∠APB取得最大值时P点的坐标.分析 如图所示,设P(x,0),x>0.则tan∠APO=$\frac{a}{x}$,tan∠BPO=$\frac{b}{x}$.tan∠APB=tan(∠APO-∠BPO),展开利用基本不等式的性质即可得出.
解答 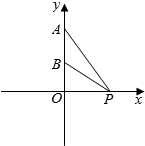 解:如图所示,
解:如图所示,
设P(x,0),x>0.
则tan∠APO=$\frac{a}{x}$,tan∠BPO=$\frac{b}{x}$.
∴tan∠APB=tan(∠APO-∠BPO)=$\frac{\frac{a}{x}-\frac{b}{x}}{1+\frac{a}{x}•\frac{b}{x}}$=$\frac{a-b}{x+\frac{ab}{x}}$≤$\frac{a-b}{2\sqrt{x•\frac{ab}{x}}}$=$\frac{a-b}{2\sqrt{ab}}$,当且仅当x=$\sqrt{ab}$时取等号.
此时P$(\sqrt{ab},0)$,∠APB取得最大值arctan$\frac{a-b}{2\sqrt{ab}}$.
点评 本题考查了和差公式、基本不等式的性质、斜率计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
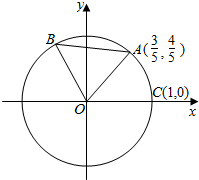 已知A、B是单位圆O上的点,且点B在第二象限,点C是圆O与x轴正半轴的交点,点A的坐标为$(\frac{3}{5},\frac{4}{5})$,若△AOB为正三角形.
已知A、B是单位圆O上的点,且点B在第二象限,点C是圆O与x轴正半轴的交点,点A的坐标为$(\frac{3}{5},\frac{4}{5})$,若△AOB为正三角形.