题目内容
若sin（
+θ）=
，求.
．
| 3π |
| 2 |
| 1 |
| 4 |
| cos(θ-2π) | ||
sin(
|
考点：三角函数的化简求值
专题：三角函数的求值
分析：利用诱导公式化简已知条件．然后化简所求表达式，代入求解即可．
解答：
解：因为sin（
+θ）=
，所以cosθ=-
．
原式=
=-
=-
=-
=
．
| 3π |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
原式=
| cosθ |
| cosθ(-cosθ)+cosθ |
| cosθ |
| cosθ(cosθ-1) |
| 1 |
| cosθ-1 |
| 1 | ||
-
|
| 4 |
| 5 |
点评：本题考查三角函数的化简求值，诱导公式的应用，考查计算能力．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
相关题目
已知角α终边上点P的坐标是（-1，m），且sinα=
，则m的值是（ ）
| ||
| 2 |
| A、-3 | ||
| B、3 | ||
C、
| ||
D、-
|
α∈[0，2π]，且
+
=sinα-cosα，则α∈（ ）
| 1-cos2α |
| 1-sin2α |
A、[0，
| ||
B、[
| ||
C、[π，
| ||
D、[
|
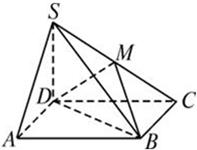如图，ABCD是平行四边形，S是平面ABCD外一点，M为SC的中点．求证：SA∥平面MDB．
