题目内容
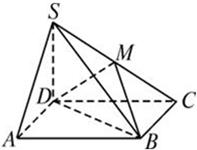如图，ABCD是平行四边形，S是平面ABCD外一点，M为SC的中点．求证：SA∥平面MDB．考点：直线与平面平行的判定
专题：证明题,空间位置关系与距离
分析：证明SA∥平面MDB，只需证明SA平行于平面MDB内的一条直线即可，而M为中点，所以连接AC、BD交于点O．由条件知道O为AC中点，从而MO为三角形SAC的中位线，从而得到SA∥OM，得证．
解答：
证明：（1）设AC与BD的交点为O，
因为四边形ABCD是平行四边形，所以O为AC的中点，
又M为SC的中点，所以，OM为三角形SAC的中位线，
所以SA∥OM，
又OM?面MDB，SA?面MDB，
所以，SA∥平面MDB．
证明：（1）设AC与BD的交点为O，因为四边形ABCD是平行四边形，所以O为AC的中点，
又M为SC的中点，所以，OM为三角形SAC的中位线，
所以SA∥OM，
又OM?面MDB，SA?面MDB，
所以，SA∥平面MDB．
点评：本题考查线面平行的判定，将线面平行转化为线线平行是解题的关键．
练习册系列答案
相关题目
已知数列{an}，满足an+1=
，若a1=
，则a2014=（ ）
| 1 |
| 1-an |
| 1 |
| 2 |
A、
| ||
| B、2 | ||
| C、-1 | ||
| D、1 |
若函数y=|cosx|，（x＞0）与直线y=kx有且仅有两个公共点，其横坐标分别为α、β，且α＜β，则（ ）
A、β=
| ||
B、β=
| ||
C、β=
| ||
D、β=-
|
关于直线a，b以及平面M，N，下列命题中正确的是（ ）
| A、若a∥M，b∥M，则a∥b |
| B、若b∥M，a⊥b，则a⊥M |
| C、若b?M，a⊥b，则a⊥M |
| D、若a⊥M，a?N，则M⊥N |