题目内容
17．已知直线经过直线3x+4y-2=0与直线2x+y+2=0的交点P，并且垂直于直线x-2y-1=0．（Ⅰ）求交点P的坐标；
（Ⅱ）求直线的方程．
分析 （Ⅰ）联立方程，求交点P的坐标；
（Ⅱ）求出直线的斜率，即可求直线的方程．
解答 解：（Ⅰ）由$\left\{\begin{array}{l}3x+4y-2=0\\ 2x+y+2=0\end{array}\right.$得$\left\{\begin{array}{l}x=-2\\ y=2\end{array}\right.$
所以P（-2，2）．--------------------------------------------------（5分）
（Ⅱ）因为直线与直线x-2y-1=0垂直，
所以kl=-2，
所以直线的方程为2x+y+2=0．----------------------------------------（8分）
点评 本题考查两方程的焦点，考查直线方程，属于中档题．
练习册系列答案
53随堂测系列答案
相关题目
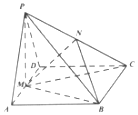已知四棱锥P-ABCD的底面ABCD是菱形，∠ADC=120°，AD的中点M是顶点P的底面ABCD的射影，N是PC的中点．
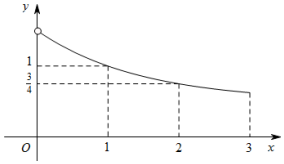已知函数f（x）是定义在[-3，0）∪（0，3]上的奇函数，当x∈（0，3]时，f（x）的图象如图所示，那么满足不等式f（x）≥2x-1 的x的取值范围是[-3，-2]∪[0，1]．
12．直线x-y-1=0的倾斜角是（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{2}$ |
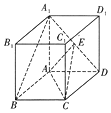如图，在底面是菱形的四棱柱ABCD-A1B1C1D1中，∠ABC=60°，AA1=AC=2，A1B=A1D=2$\sqrt{2}$，点E在A1D上，且E为A1D的中点
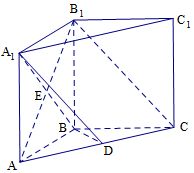如图，在直三棱柱ABC-A1B1C1中，AB=BC=BB1，AB1∩A1B=E，D为AC上的点，B1C∥平面A1BD；