题目内容

2．《张丘建算经》是我国南北朝时期的一部重要数学著作，书中系统的介绍了等差数列，同类结果在三百多年后的印度才首次出现．书中有这样一个问题，大意为：某女子善于织布，后一天比前一天织得快，而且每天增加的数量相同，已知第一天织布4尺，半个月（按15天计算）总共织布81尺，问每天增加的数量为多少尺？该问题的答案为$\frac{1}{5}$．

分析 每天增加的数量为d尺，利用等差数列前n项和公式列出方程组，能求出公差d．

解答 解：每天增加的数量为d尺，
由题意得：
${S}_{15}=15×4+\frac{15×14}{2}d=81$，
解得d=$\frac{1}{5}$．
故答案为：$\frac{1}{5}$．

点评 本题考查等差数列的公差的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．

练习册系列答案
相关题目
12．下列命题中的假命题是（　　）
A．?x∈R，x2≥0B．?x∈R，2x-1＞0
C．?x∈R，lgx＜1D．?x∈R，sinx+cosx=2
13．原点到直线4x+3y-1=0的距离为$\frac{1}{5}$．
10．已知元素为实数的集合S满足下列条件：①0∉S，1∉S；②若a∈S，则$\frac{1}{1-a}$∈S．
（Ⅰ）若{2，-2}⊆S，求使元素个数最少的集合S；
（Ⅱ）若非空集合S为有限集，则你对集合S的元素个数有何猜测？并请证明你的猜测正确．
17．已知直线经过直线3x+4y-2=0与直线2x+y+2=0的交点P，并且垂直于直线x-2y-1=0．
（Ⅰ）求交点P的坐标；
（Ⅱ）求直线的方程．
7．已知p：|x-1|＜2，q：f（x）=$\frac{{x}^{2}+1}{x}$的最小值为2，则p是q的（　　）
A．充分而不必要条件B．充要条件
C．必要而不充分条件D．既不充分也不必要条件
14．已知函数f（x）=$\left\{\begin{array}{l}{{2}^{x}，x∈（-∞，0]}\\{{x}^{2}+2ax+1，x∈（0，+∞）}\end{array}\right.$，若函数g（x）=f（x）+2x-a有三个零点，则实数a的取值范围是（　　）
A．（0，+∞）B．（-∞，-1）C．（-∞，-3）D．（0，-3）
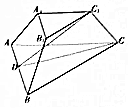11．已知三棱台ABC-A1B1C1中，AB=BC=4，AC=2A1C1=2$\sqrt{2}$，AA1=CC1=1，平面AA1B1B⊥平面AA1C1C．
（1）求证：BB1⊥平面AA1C1C；
（2）点D为AB上一点，二面角D-CC1-B的大小为30°，求BC与平面DCC1所成角的正弦值．
12．若x＞2m2-3是-1＜x＜4的必要不充分条件，则实数m的取值范围是（　　）
A．[-3，3]B．（-∞，-3]∪[3，+∞）C．（-∞，-1]∪[1，+∞）D．[-1，1]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网