题目内容
5.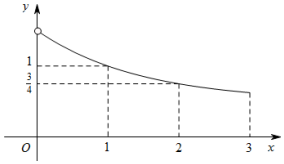 已知函数f(x)是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x)的图象如图所示,那么满足不等式f(x)≥2x-1 的x的取值范围是[-3,-2]∪[0,1].
已知函数f(x)是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x)的图象如图所示,那么满足不等式f(x)≥2x-1 的x的取值范围是[-3,-2]∪[0,1].
分析 由图象可知,当x∈(0,3]时,f(x)单调递减,当x∈[-3,0)时,f(x)单调递减,分别利用函数的图象,结合不等式f(x)≥2x-1,即可得出结论.
解答 解:由图象可知,x=0时,2x-1=0,∴f(x)≥0,成立;
当x∈(0,3]时,f(x)单调递减,
当0<x≤1时,f(x)>1,2x-1≤1,满足不等式f(x)≥2x-1;
当1<x<3时,f(x)<1,1<2x-1<7,不满足不等式f(x)≥2x-1;
∵函数f(x) 是定义在[-3,0)∪(0,3]上的奇函数,
∴当x∈[-3,0)时,f(x)单调递减,
当-3<x≤-2时,-$\frac{3}{4}$≤f(x)<0,-$\frac{7}{8}$<2x-1≤-$\frac{3}{4}$,满足不等式f(x)≥2x-1;
当x>-2时,f(x)<-$\frac{3}{4}$,2x-1>-$\frac{3}{4}$,不满足不等式f(x)≥2x-1;
∴满足不等式f(x)≥2x-1 的x的取值范围是[-3,-2]∪[0,1].
故答案为:[-3,-2]∪[0,1].
点评 本题考查不等式的解法,考查数形结合的数学思想,考查学生分析解决问题的能力,正确运用函数的图象是关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
16. 如图,三棱柱ABC-A1B1C1的各棱长均为2,且侧棱与底面垂直,其正(主)视图如图所示,则此三棱柱侧(左)视图的面积为( )
如图,三棱柱ABC-A1B1C1的各棱长均为2,且侧棱与底面垂直,其正(主)视图如图所示,则此三棱柱侧(左)视图的面积为( )
 如图,三棱柱ABC-A1B1C1的各棱长均为2,且侧棱与底面垂直,其正(主)视图如图所示,则此三棱柱侧(左)视图的面积为( )
如图,三棱柱ABC-A1B1C1的各棱长均为2,且侧棱与底面垂直,其正(主)视图如图所示,则此三棱柱侧(左)视图的面积为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 4 |
20.下列函数中,在区间($\frac{π}{2}$,π)上为增函数的是( )
| A. | y=sinx | B. | y=cosx | C. | y=tanx | D. | y=-tanx |
14.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x},x∈(-∞,0]}\\{{x}^{2}+2ax+1,x∈(0,+∞)}\end{array}\right.$,若函数g(x)=f(x)+2x-a有三个零点,则实数a的取值范围是( )
| A. | (0,+∞) | B. | (-∞,-1) | C. | (-∞,-3) | D. | (0,-3) |