题目内容
 如图,直三棱柱ABC-A1B1C1的底面ABC是等腰直角三角形,AB=AC=1,侧棱AA1⊥底面ABC,且AA1=2,E是BC的中点,F是A1C上的点.
如图,直三棱柱ABC-A1B1C1的底面ABC是等腰直角三角形,AB=AC=1,侧棱AA1⊥底面ABC,且AA1=2,E是BC的中点,F是A1C上的点.(1)求异面直线AE与A1C所成角θ的大小(结果用反三角函数表示);
(2)若EF⊥A1C,求线段CF的长.
考点:异面直线及其所成的角
专题:空间位置关系与距离
分析:(1)取B1C1的中点E1,连A1E1,则A1E1∥AE,即∠CA1E1即为异面直线AE与A1C所成的角θ,连结E1C,解三角形可得异面直线AE与A1C所成角θ的大小,
(2)以A为原点,建立如图空间直角坐标系,设CF的长为x,根据EF⊥A1C,对应向量的数量积为0,构造关于x的方程,解方程可得线段CF的长.
(2)以A为原点,建立如图空间直角坐标系,设CF的长为x,根据EF⊥A1C,对应向量的数量积为0,构造关于x的方程,解方程可得线段CF的长.
解答:
 解:(1)取B1C1的中点E1,连A1E1,则A1E1∥AE,
解:(1)取B1C1的中点E1,连A1E1,则A1E1∥AE,
即∠CA1E1即为异面直线AE与A1C所成的角θ.…(2分)
连结E1C.
在Rt△E1C1C中,由E1C1=
,CC1=2
知A1C=
=
在Rt△A1C1C中,由A1C1=1,CC1=2知A1C=
…(4分)
在△A1E1C中,cosθ=
=
=
∴θ=arccos
…(6分)
(2)以A为原点,建立如图空间直角坐标系,设CF的长为x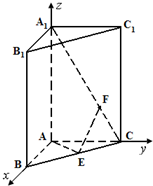
则各点的坐标为,E(
,
,0),F(0,1-
x,
x),A1(0,0,2),C(0,1,0)…(2分)
∴
=(-
,
-
x,
x),
=(0,1,-2)
由EF⊥A1C知
•
=0…(4分)
即
-
x-2•
x=0,解得x=
∴线段CF的长为
…(6分)
 解:(1)取B1C1的中点E1,连A1E1,则A1E1∥AE,
解:(1)取B1C1的中点E1,连A1E1,则A1E1∥AE,即∠CA1E1即为异面直线AE与A1C所成的角θ.…(2分)
连结E1C.
在Rt△E1C1C中,由E1C1=
| ||
| 2 |
知A1C=
|
3
| ||
| 2 |
在Rt△A1C1C中,由A1C1=1,CC1=2知A1C=
| 5 |
在△A1E1C中,cosθ=
(
| ||||||||||
2•
|
| 1 | ||
|
| ||
| 10 |
∴θ=arccos
| ||
| 10 |
(2)以A为原点,建立如图空间直角坐标系,设CF的长为x

则各点的坐标为,E(
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 5 |
2
| ||
| 5 |
∴
| EF |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 5 |
2
| ||
| 5 |
| A1C |
由EF⊥A1C知
| EF |
| A1C |
即
| 1 |
| 2 |
| ||
| 5 |
2
| ||
| 5 |
| ||
| 10 |
∴线段CF的长为
| ||
| 10 |
点评:本题考查的知识点是异面直线及其所成的角,空间向量垂直,难度不大,属于基础题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
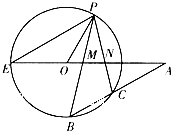 如图,E,P,B,C为圆O上的四点,直线PB,PC,BC分别交直线EO于M,N三点,且PM=PN.
如图,E,P,B,C为圆O上的四点,直线PB,PC,BC分别交直线EO于M,N三点,且PM=PN.