题目内容
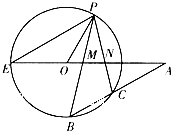 如图,E,P,B,C为圆O上的四点,直线PB,PC,BC分别交直线EO于M,N三点,且PM=PN.
如图,E,P,B,C为圆O上的四点,直线PB,PC,BC分别交直线EO于M,N三点,且PM=PN.(Ⅰ)求证:∠POA+∠BAO=90°;
(Ⅱ)若BC∥PE,求
| PE |
| PO |
考点:圆內接多边形的性质与判定,平行线分线段成比例定理
专题:立体几何
分析:(Ⅰ)过点P作圆O的切线交直线EO于F点,由弦切角性质可知∠NPF=∠PBA,结合PM=PN,可得∠PFN=∠BAO,进而根据切线的性质得到∠POA+∠PFN=90°,等量代换后,得到答案.
(Ⅱ)若BC∥PE,则∠PEO=∠BAO,又∠POA=2∠PEO,可得∠POA=2∠BAO,结合(I)中结论可求出∠BAO=30°,解三角形可得答案.
(Ⅱ)若BC∥PE,则∠PEO=∠BAO,又∠POA=2∠PEO,可得∠POA=2∠BAO,结合(I)中结论可求出∠BAO=30°,解三角形可得答案.
解答:
证明:(Ⅰ)过点P作圆O的切线交直线EO于F点,由弦切角性质可知∠NPF=∠PBA,
∵PM=PN,
∴∠PNO=∠PMA,
则∠PNO-∠NPF=∠PMA-∠PBA,
即∠PFN=∠BAO.
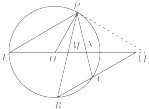
又PF为圆O的切线,故∠POA+∠PFN=90°,
故∠POA+∠BAO=90°.…(5分)
解:(Ⅱ)若BC∥PE,则∠PEO=∠BAO,又∠POA=2∠PEO,
故∠POA=2∠BAO,
由(Ⅰ)可知90°=∠POA+∠BAO=3∠BAO,故∠BAO=30°,
则∠PEO=∠BAO=30°,cos∠PEO=
,即
=
,
故
=
=
.…(10分)
∵PM=PN,
∴∠PNO=∠PMA,
则∠PNO-∠NPF=∠PMA-∠PBA,
即∠PFN=∠BAO.

又PF为圆O的切线,故∠POA+∠PFN=90°,
故∠POA+∠BAO=90°.…(5分)
解:(Ⅱ)若BC∥PE,则∠PEO=∠BAO,又∠POA=2∠PEO,
故∠POA=2∠BAO,
由(Ⅰ)可知90°=∠POA+∠BAO=3∠BAO,故∠BAO=30°,
则∠PEO=∠BAO=30°,cos∠PEO=
| ||
| EO |
| ||
| 2 |
| PE |
| 2EO |
故
| PE |
| PO |
| PE |
| EO |
| 3 |
点评:本题考查的知识点是弦切角定理,切线的性质,圆心角定理,是平面几何证明的简单综合应用,难度中档.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知底面圆半径为4的圆锥SO中,S为顶点,O为底面圆心,SB、SC是母线,∠BOC=120°,作OA⊥SC于A点,若将△SAO绕轴旋转一周所得几何体的体积是圆锥SO体积的
如图,已知底面圆半径为4的圆锥SO中,S为顶点,O为底面圆心,SB、SC是母线,∠BOC=120°,作OA⊥SC于A点,若将△SAO绕轴旋转一周所得几何体的体积是圆锥SO体积的 如图,直三棱柱ABC-A1B1C1的底面ABC是等腰直角三角形,AB=AC=1,侧棱AA1⊥底面ABC,且AA1=2,E是BC的中点,F是A1C上的点.
如图,直三棱柱ABC-A1B1C1的底面ABC是等腰直角三角形,AB=AC=1,侧棱AA1⊥底面ABC,且AA1=2,E是BC的中点,F是A1C上的点.