题目内容
安徽省第13届运动会在安庆举行,为了更好地做好服务工作,需对所有的志愿者进行赛前培训,培训结束后,所有志愿者参加了“综合素质”和“服务技能”两个科目的考试,成绩分为A,B,C,D,E五个等级.某考场考生的两科考试成绩数据统计如下图所示,其中“综合素质”科目的成绩为B的考生有10人.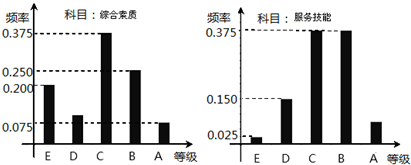
(1)求该考场考生中“综合素质”科目中成绩为A的人数;
(2)若等级A,B,C,D,E分别对应90分,80分,70分,60分,50分,若该场考生的平均成绩不低于60分则认为培训合格,问该场考试综合素质培训是否合格,并说明理由.
(3)已知参加本考场测试的考生中,恰有两人的两科成绩均为A.在至少一科成绩为A的考生中,随机抽取两人进行访谈,求这两人的两科成绩均为A的概率.

(1)求该考场考生中“综合素质”科目中成绩为A的人数;
(2)若等级A,B,C,D,E分别对应90分,80分,70分,60分,50分,若该场考生的平均成绩不低于60分则认为培训合格,问该场考试综合素质培训是否合格,并说明理由.
(3)已知参加本考场测试的考生中,恰有两人的两科成绩均为A.在至少一科成绩为A的考生中,随机抽取两人进行访谈,求这两人的两科成绩均为A的概率.
考点:列举法计算基本事件数及事件发生的概率,频率分布直方图
专题:概率与统计
分析:(Ⅰ)根据“综合素质”科目中成绩等级为B的考生人数,结合样本容量=频数÷频率得出该考场考生人数,从而得到该考场考生中“服务技能”科目中成绩等级为A的人数.
(Ⅱ)利用平均数公式即可计算该考场考生“综合素质”科目的平均分,即可得到答案.
(Ⅲ)通过列举的方法计算出选出的2人所有可能的情况及这两人的两科成绩等级均为A的情况;利用古典概型概率公式求出随机抽取两人进行访谈,这两人的两科成绩等级均为A的概率
(Ⅱ)利用平均数公式即可计算该考场考生“综合素质”科目的平均分,即可得到答案.
(Ⅲ)通过列举的方法计算出选出的2人所有可能的情况及这两人的两科成绩等级均为A的情况;利用古典概型概率公式求出随机抽取两人进行访谈,这两人的两科成绩等级均为A的概率
解答:
解:(Ⅰ)因为“综合素质”科目中成绩等级为B的考生有10人,
所以该考场有10÷0.25=40人,
所以该考场考生中“综合素质”科目中成绩等级为A的人数为:40×0.075=3人;
(Ⅱ)该考场考生“综合素质”科目的平均分为:
×[50×(40×0.2)+60×(40×0.1)+70×(40×0.375)+80×(40×0.25)+90×(40×0.075)]=69;
(Ⅲ)因为两科考试中,共有6人得分等级为A,又恰有两人的两科成绩等级均为A,
所以还有2人只有一个科目得分为A,
设这四人为甲,乙,丙,丁,其中甲,乙是两科成绩都是A的同学,
则在至少一科成绩等级为A的考生中,随机抽取两人进行访谈,基本事件空间为:
Ω={{甲,乙},{甲,丙},{甲,丁},{乙,丙},{乙,丁},{丙,丁}},一共有6个基本事件.
设“随机抽取两人进行访谈,这两人的两科成绩等级均为A”为事件B,所以事件B中包含的基本事件有1个,
则P(B)=
.
所以该考场有10÷0.25=40人,
所以该考场考生中“综合素质”科目中成绩等级为A的人数为:40×0.075=3人;
(Ⅱ)该考场考生“综合素质”科目的平均分为:
| 1 |
| 40 |
(Ⅲ)因为两科考试中,共有6人得分等级为A,又恰有两人的两科成绩等级均为A,
所以还有2人只有一个科目得分为A,
设这四人为甲,乙,丙,丁,其中甲,乙是两科成绩都是A的同学,
则在至少一科成绩等级为A的考生中,随机抽取两人进行访谈,基本事件空间为:
Ω={{甲,乙},{甲,丙},{甲,丁},{乙,丙},{乙,丁},{丙,丁}},一共有6个基本事件.
设“随机抽取两人进行访谈,这两人的两科成绩等级均为A”为事件B,所以事件B中包含的基本事件有1个,
则P(B)=
| 1 |
| 6 |
点评:本小题主要考查统计与概率的相关知识,具体涉及到频率分布直方图、平均数及古典概型等内容

练习册系列答案
相关题目
 如图F1,F2为双曲线C:
如图F1,F2为双曲线C:| x2 |
| a2 |
| y2 |
| b2 |
| A、5 | B、30 | C、225 | D、15 |
如图是一个算法的流程图,若输出的结果是255,则判断框中的整数N的值为( )


| A、6 | B、7 | C、8 | D、9 |
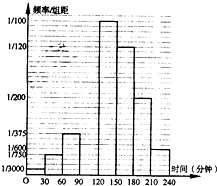 为了调查学生星期天晚上学习时间利用问题,某校从高二年级1000名学生(其中走读生450名,住宿生500名)中,采用分层抽样的方法抽取n名学生进行问卷调查.根据问卷取得了这n名同学每天晚上学习时间(单位:分钟)的数据,按照以下区间分为八组①[0,30),②[30,60),③[60,90),④[90,120),⑤[120,150),⑥[150,180),⑦[180,210),⑧[210,240],得到频率分布直方图如图所示.已知抽取的学生中星期天晚上学习时间少于60分钟的人数为5人;
为了调查学生星期天晚上学习时间利用问题,某校从高二年级1000名学生(其中走读生450名,住宿生500名)中,采用分层抽样的方法抽取n名学生进行问卷调查.根据问卷取得了这n名同学每天晚上学习时间(单位:分钟)的数据,按照以下区间分为八组①[0,30),②[30,60),③[60,90),④[90,120),⑤[120,150),⑥[150,180),⑦[180,210),⑧[210,240],得到频率分布直方图如图所示.已知抽取的学生中星期天晚上学习时间少于60分钟的人数为5人;