题目内容
已知a，b∈R+，求证：a+b≤
•
．
| 2 |
| a2+b2 |
考点：不等式的证明
专题：证明题,不等式的解法及应用
分析：利用基本不等式可得a2+b2≥2ab，从而可得2（a2+b2）≥（a+b）2，即可证明结论．
解答：
解：∵a，b∈R+，a2+b2≥2ab，
∴2（a2+b2）≥a2+b2+2ab，
∴2（a2+b2）≥（a+b）2，
∴a+b≤
•
．
∴2（a2+b2）≥a2+b2+2ab，
∴2（a2+b2）≥（a+b）2，
∴a+b≤
| 2 |
| a2+b2 |
点评：本题考查不等式的证明，考查基本不等式的运用，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
已知等差数列{an}满足a2=3，an-1=17（n≥2），Sn=100，则n的值为（ ）
| A、10 | B、9 | C、8 | D、11 |
“x＜1”是“log2（x+1）＜1”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
经过双曲线
-
=1（a＞b＞0）的右焦点为F作该双曲线一条渐近线的垂线与两条渐近线相交于M，N两点，若O是坐标原点，△OMN的面积是
a2，则该双曲线的离心率是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
已知抛物线y2=4x与双曲线
-
=1（a＞0，b＞0）有相同的焦点F，点A，B是两曲线的交点，若（
+
）•
=0，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| OA |
| OB |
| AF |
A、
| ||
B、
| ||
C、
| ||
D、
|
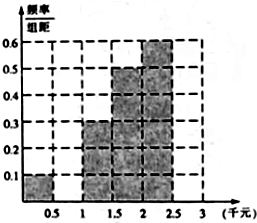2014年7月16日，中国互联网络信息中心发布《第三十四次中国互联网发展状况报告》，报告显示：我国网络购物用户已达3.32亿．为了了解网购者一次性购物金额情况，某统计部门随机抽查了6月1日这一天100名网购者的网购情况，得到如下数据统计表．已知网购金额在2000元以上（不含2000元）的频率为0.4．