题目内容
7.已知(1+i)i=a+bi(a,b∈R),其中i为虚数单位,则a+b的值为( )| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
分析 直接由复数代数形式的乘法运算化简(1+i)i,再由复数相等的条件即可求出a、b的值,则a+b的值可求.
解答 解:由(1+i)i=i+i2=-1+i=a+bi(a,b∈R),
得a=-1,b=1.
则a+b=-1+1=0.
故选:B.
点评 本题考查了复数代数形式的乘除运算,考查了复数相等的条件,是基础题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
17.如图,在菱形ABCD中,AB=2,∠DAB=60°,E为CD的中点,则$\overrightarrow{AD}$•$\overrightarrow{AE}$的值是( )
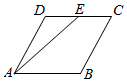

| A. | $\sqrt{7}$ | B. | 5 | C. | $\sqrt{21}$ | D. | 6 |
18.设集合M={x|0≤x<1},集合N={x|x2-2x-3≥0},则集合M∩(∁RN)=( )
| A. | {x|0≤x<1} | B. | {x|0≤x<2} | C. | {x|0≤x≤1} | D. | {x|0≤x≤2} |
2.已知复数z=$\frac{10-5ai}{1-2i}$的实部与虚部之和为4,则复数z在复平面上对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
12.函数f(x)=sin(2x+φ)(|φ|<$\frac{π}{2}$)的图象向右平移$\frac{π}{12}$个单位后的图象关于y轴对称,则函数f(x)在[0,$\frac{π}{4}$]上的最大值为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
17.已知$\vec a$=(-1,3),$\vec b$=(1,t),若($\vec a$-2$\vec b$)⊥$\vec a$,则|${\vec b}$|=( )
| A. | 5 | B. | $\sqrt{2}$ | C. | $\sqrt{10}$ | D. | $\sqrt{5}$ |
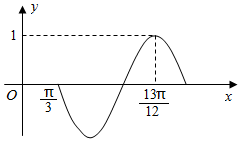 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.