题目内容
已知椭圆C的一个焦点为F(-2,0),且长轴长与短轴长的比是2:
.
(1)求椭圆C的标准方程;
(2)设点M(m,0)在椭圆C的长轴上,点P是椭圆上任意一点,记|
|的最小值为f(m)若关于实数m的方程f(m)-2t=0有解,请求实数t的取值范围.
| 3 |
(1)求椭圆C的标准方程;
(2)设点M(m,0)在椭圆C的长轴上,点P是椭圆上任意一点,记|
| MP |
考点:直线与圆锥曲线的关系,椭圆的标准方程,椭圆的简单性质
专题:圆锥曲线中的最值与范围问题
分析:(1)设椭圆C的方程为
+
=1(a>b>0),由题意得
,由此能求出椭圆C的方程.
(2)设P(x,y)为椭圆上的动点,由于椭圆方程为
+
=1,由|
|2=(x-m)2+y2=
(x-4m)2+12-3m2,由此能求出|
|的最小值实数t的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
|
(2)设P(x,y)为椭圆上的动点,由于椭圆方程为
| x2 |
| 16 |
| y2 |
| 12 |
| MP |
| 1 |
| 4 |
| MP |
解答:
解:(1)设椭圆C的方程为
+
=1(a>b>0).
由题意,得
,
解得a2=16,b2=12.
∴椭圆C的方程为
+
=1.
(2)设P(x,y)为椭圆上的动点,由于椭圆方程为
+
=1,∴-4≤x≤4,
∵
=(x-m,y),
∴|
|2=(x-m)2+y2=(x-m)2+12×(1-
)
=
x2-2mx+m2+12
=
(x-4m)2+12-3m2,
∵
,
∴|
|的最小值f(m)=
,
∴f(m)的值域为[0,2
],
又由f(m)-2t=0,得2t=f(m),
∴0≤2t≤2
,
故实数t的取值范围为[0,
].
| x2 |
| a2 |
| y2 |
| b2 |
由题意,得
|
解得a2=16,b2=12.
∴椭圆C的方程为
| x2 |
| 16 |
| y2 |
| 12 |
(2)设P(x,y)为椭圆上的动点,由于椭圆方程为
| x2 |
| 16 |
| y2 |
| 12 |
∵
| MP |
∴|
| MP |
| x2 |
| 16 |
=
| 1 |
| 4 |
=
| 1 |
| 4 |
∵
|
∴|
| MP |
|
∴f(m)的值域为[0,2
| 3 |
又由f(m)-2t=0,得2t=f(m),
∴0≤2t≤2
| 3 |
故实数t的取值范围为[0,
| 3 |
点评:本题考查椭圆方程的标准方程的求法,考查实数的取值范围的求法,是中档题,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
相关题目
把十进制数11化为二进制数的结果是( )
| A、1011(2) |
| B、1101(2) |
| C、1110(2) |
| D、1111(2) |
等差数列{an}前n项和Sn,满足S20=S40,下列结论正确的是( )
| A、S30是Sn中的最大值 |
| B、S20是Sn中的最小值 |
| C、S30=0 |
| D、S60=0 |
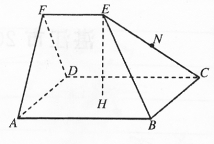 如图,五面体EF-ABCD中,ABCD是以点H为中心的正方形,EF∥AB,EH丄平面 ABCD,AB=2,EF=EH=1.
如图,五面体EF-ABCD中,ABCD是以点H为中心的正方形,EF∥AB,EH丄平面 ABCD,AB=2,EF=EH=1.