题目内容
16.设m∈R,若函数f(x)=(m+1)x${\;}^{\frac{2}{3}}$+mx+1是偶函数,则f(x)的单调递增区间是[0,+∞).分析 由题意函数f(x)=(m+1)x${\;}^{\frac{2}{3}}$+mx+1是偶函数,则mx=0,可得m=0,可得f(x)=x${\;}^{\frac{2}{3}}$+1,可求单调递增区间.
解答 解:由题意:函数f(x)=(m+1)x${\;}^{\frac{2}{3}}$+mx+1是偶函数,
则mx=0,故得m=0,
那么:f(x)=x${\;}^{\frac{2}{3}}$+1,
根据幂函数的性质可知:
函数f(x)的单点增区间为[0,+∞).
故答案为:[0,+∞).
点评 本题考查了幂函数的图象及性质的运用.属于基础题.

练习册系列答案
相关题目
7.若锐角α满足cos(α+$\frac{π}{4}$)=$\frac{3}{5}$,则sin2α=( )
| A. | $\frac{7}{25}$ | B. | $\frac{16}{25}$ | C. | $\frac{18}{25}$ | D. | $\frac{24}{25}$ |
20.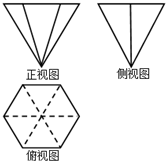 一个几何体的三视图如图所示,其中正视图是边长为2的等边三角形,俯视图为正六边形,则该几何体的侧视图的面积是( )
一个几何体的三视图如图所示,其中正视图是边长为2的等边三角形,俯视图为正六边形,则该几何体的侧视图的面积是( )
 一个几何体的三视图如图所示,其中正视图是边长为2的等边三角形,俯视图为正六边形,则该几何体的侧视图的面积是( )
一个几何体的三视图如图所示,其中正视图是边长为2的等边三角形,俯视图为正六边形,则该几何体的侧视图的面积是( )| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
1.如图所示,在四面体中,若直线EF和GH相交,则它们的交点一定( )


| A. | 在直线DB上 | B. | 在直线AB上 | C. | 在直线CB上 | D. | 都不对 |
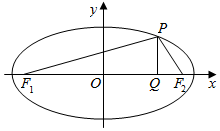 已知椭圆Г:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1、F2,P是椭圆上位于第一象限内的点,PQ⊥x轴,垂足为Q,且|F1F2|=6,∠PF1F2=arccos$\frac{5\sqrt{3}}{9}$,△PF1F2的面积为3$\sqrt{2}$.
已知椭圆Г:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1、F2,P是椭圆上位于第一象限内的点,PQ⊥x轴,垂足为Q,且|F1F2|=6,∠PF1F2=arccos$\frac{5\sqrt{3}}{9}$,△PF1F2的面积为3$\sqrt{2}$.