已知椭圆Г:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的左.右两个焦点分别为F1.F2.P是椭圆上位于第一象限内的点.PQ⊥x轴.垂足为Q.且|F1F2|=6.∠PF1F2=arccos$\frac{5\sqrt{3}}{9}$.△PF1F2的面积为3$\sqrt{2}$．(1)求椭圆Г的方程,(2)若M是椭圆上的动� 题目和参考答案——青夏教育精英家教网—

题目内容

1．

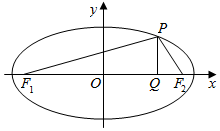已知椭圆Г：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右两个焦点分别为F₁、F₂，P是椭圆上位于第一象限内的点，PQ⊥x轴，垂足为Q，且|F₁F₂|=6，∠PF₁F₂=arccos$\frac{5\sqrt{3}}{9}$，△PF₁F₂的面积为3$\sqrt{2}$．
（1）求椭圆Г的方程；
（2）若M是椭圆上的动点，求|MQ|的最大值．并求出|MQ|取得最大值时M的坐标．

分析由

解答解：（1）由△PF₁F₂的面积为3$\sqrt{2}$，|F₁F₂|=6，
得$\frac{1}{2}×6×{y}_{P}=3\sqrt{2}$，∴${y}_{P}=\sqrt{2}$，
又∠PF₁F₂=arccos$\frac{5\sqrt{3}}{9}$，∴$|{F}_{1}Q|=\frac{5\sqrt{3}}{9}|P{F}_{1}|$，
则由$（\frac{5\sqrt{3}}{9}|P{F}_{1}|）^{2}+（\sqrt{2}）^{2}=|P{F}_{1}{|}^{2}$，解得$|P{F}_{1}|=3\sqrt{3}$．
∴$|P{F}_{2}{|}^{2}=|P{F}_{1}{|}^{2}+4{c}^{2}-2•2c•|P{F}_{1}|•\frac{5\sqrt{3}}{9}$，解得：$|P{F}_{2}|=\sqrt{3}$．
∴2a=4$\sqrt{3}$，a=2$\sqrt{3}$，c=3，b²=a²-c²=3．
∴椭圆Г的方程为$\frac{{x}^{2}}{12}+\frac{{y}^{2}}{3}=1$；
（2）由（1）知，${y}_{P}=\sqrt{2}$，代入$\frac{{x}^{2}}{12}+\frac{{y}^{2}}{3}=1$，可得x_p=2，
∴Q（2，0），设M（x₀，y₀），则$\frac{{{x}_{0}}^{2}}{12}+\frac{{{y}_{0}}^{2}}{3}=1$，∴${{y}_{0}}^{2}=3-\frac{{{x}_{0}}^{2}}{4}$．
∴|MQ|=$\sqrt{（{x}_{0}-2）^{2}+{{y}_{0}}^{2}}$=$\sqrt{{{x}_{0}}^{2}-4{x}_{0}+4+3-\frac{{{x}_{0}}^{2}}{4}}$=$\sqrt{\frac{3}{4}{{x}_{0}}^{2}-4{x}_{0}+7}$．
∵$-2\sqrt{3}≤{x}_{0}≤2\sqrt{3}$，∴当${x}_{0}=-2\sqrt{3}$时，$|MQ{|}_{max}=\sqrt{16+8\sqrt{3}}$．