题目内容
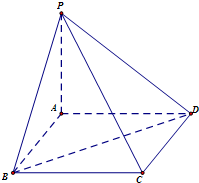 如图,已知ABCD是正方形;P是平面ABCD外一点,且PA⊥面ABCD,PA=AB=3.求:
如图,已知ABCD是正方形;P是平面ABCD外一点,且PA⊥面ABCD,PA=AB=3.求:(1)二面角P-CD-A的大小.
(2)三棱锥P-ABD的体积.
考点:棱柱、棱锥、棱台的体积,异面直线及其所成的角
专题:空间位置关系与距离
分析:(1)连结AC,BD,由正方形性质得AC⊥BD,由线面垂直得BD⊥PA,从而BD⊥平面PAC,由此能求出BD与PC的夹角为90°.
(2)由已知条件得PA是三棱锥P-ABD的高,由此能求出三棱锥P-ABD的体积.
(2)由已知条件得PA是三棱锥P-ABD的高,由此能求出三棱锥P-ABD的体积.
解答:
解:(1)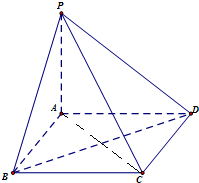 连结AC,BD,
连结AC,BD,
∵ABCD是正方形,∴AC⊥BD,
∵PA⊥面ABCD,BD?平面ABCD,
∴BD⊥PA,
∵AC∩PA=A,
∴BD⊥平面PAC,
∵PC?平面PAC,∴BD⊥PC,
∴BD与PC的夹角为90°.
(2)∵ABCD是正方形,P是平面ABCD外一点,
且PA⊥面ABCD,PA=AB=3,
∴三棱锥P-ABD的体积:
V=
×S△ABD×PA
=
×
×3×3×3
=
.
 连结AC,BD,
连结AC,BD,∵ABCD是正方形,∴AC⊥BD,
∵PA⊥面ABCD,BD?平面ABCD,
∴BD⊥PA,
∵AC∩PA=A,
∴BD⊥平面PAC,
∵PC?平面PAC,∴BD⊥PC,
∴BD与PC的夹角为90°.
(2)∵ABCD是正方形,P是平面ABCD外一点,
且PA⊥面ABCD,PA=AB=3,
∴三棱锥P-ABD的体积:
V=
| 1 |
| 3 |
=
| 1 |
| 3 |
| 1 |
| 2 |
=
| 9 |
| 2 |
点评:本题考查异面直线的夹角的求法,考查三棱锥的体积的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
直线y=kx-2与抛物线y2=6x交于A、B两点,且线段AB的中点的纵坐标为3,则k的值是( )
| A、1 | B、-2 |
| C、1或-2 | D、以上都不是 |
下列说法正确的是( )
| A、命题“?x∈R使得x2+2x+3<0”的否定是:“?x∈R,x2+2x+3>0” | ||
| B、“a>1”是“f(x)=logax(a>0,a≠1)在(0,+∞)上为增函数”的充要条件 | ||
| C、“p∧q为真命题”是“p∨q为真命题”的必要不充分条件 | ||
D、命题p:“?x∈R,sinx+cosx≤
|
等差数列x1,x2,x3,…,x11的公差为
,随机变量ξ等可能地取x1,x2,x3,…,x11,则ξ的标准差为( )
| ||
| 2 |
A、
| ||||
B、
| ||||
| C、5 | ||||
| D、10 |
 如图,已知斜三棱柱ABC-A1B1C1的底面是正三角形,点M、N分别是A1C1和A1B1的中点,AA1=AB=BM=2,∠A1AB=60°.
如图,已知斜三棱柱ABC-A1B1C1的底面是正三角形,点M、N分别是A1C1和A1B1的中点,AA1=AB=BM=2,∠A1AB=60°. 如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=2,BC=
如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=2,BC=