题目内容

等差数列x1，x2，x3，…，x11的公差为
10
2
，随机变量ξ等可能地取x1，x2，x3，…，x11，则ξ的标准差为（　　）
A、
15
11
11
B、
10
C、5
D、10
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：利用等差数列的前n项和公式可得Eξ，再利用方差的计算公式即可得出结论．
解答： 解：由题意可得Eξ=
1
11
（11x1+
11×10
2
×
10
2
）=x1+
5
10
2
．
∴xn-Eξ=x1+（n-1）d-（x1+5d）=（n-6）d，
∴Dξ=
1
11
[（-5d）2+…+（-d）2+0+d2+（2d）2+…+（5d）2]=25
∴Vξ=5
故选C．
点评：熟练掌握等差数列的前n项和公式、数学期望和方差的计算公式是解题的关键．
练习册系列答案
相关题目
设事件A=“在矩形ABCD的边CD上任取一点M，使△AMB中∠AMB为最大角”，且事件A发生的概率P（A）=
1
3
，则
AD
AB
=（　　）
A、
5
3
B、
7
4
C、
5
9
D、
1
2
在棱长为a的正方体ABCD-A1B1C1D1中，M是AA1的中点，则点A到平面MBD的距离是（　　）
A、
6
3
a
B、
3
6
a
C、
3
4
a
D、
6
6
a
若甲的运动方程为s1（t）=et-1，乙的运动方程为s2（t）=et，则当甲、乙的瞬时速度相等时，t的值等于（　　）
A、1B、2C、3D、4
下列说法正确的有（　　）
①单位向量都相等；②长度相等且方向相反的两个向量一定是共线向量；③若
a
，
b
满足|
a
|＞|
b
|且
a
与
b
同向，则
a
＞
b
；④若
a
=
b
，则|
a
|=|
b
|，反之也成立； ⑤对于任意向量
a
、
b
，必有|
a
+
b
|≤|
a
|+|
b
|．
A、①②③B、①②④
C、③④⑤D、②⑤
设函数f（x）=log2（4-x），g（x）=log2x．
（1）求f（x）的定义域；
（2）求f（x）+g（x）的值域；
（3）如果对任意的x∈[1，4]不等式（4-2g（x））•f（4-x）-k≤0求实数k的取值范围．
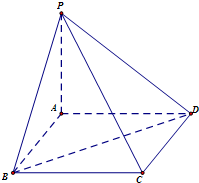如图，已知ABCD是正方形；P是平面ABCD外一点，且PA⊥面ABCD，PA=AB=3．求：
（1）二面角P-CD-A的大小．
（2）三棱锥P-ABD的体积．
记函数f（x）=
3+x
-
-x-1
的定义域为集合M，函数g（x）=x2-4x+3的值域为集合N，求：
（1）M，N；
（2）M∩N，M∪N．
如图，多面体ABCC1A1B1中，四边形AA1C1C是正方形，四边形BCC1B1是直角梯形，CC1⊥BC且BC∥B1C1．△ACB、△A1C1B1都是等腰直角三角形，A、B1分别为直角顶点，M是B1B上的点，BM=2MB1．
（1）证明CM⊥平面A1B1B；
（2）求二面角A-A1M-B的余弦值；
（3）当AA1=1时，求多面体ABCC1A1B1的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网