题目内容
设函数fn(x)=2anx3-3an+1x2+6x+1,an>0,a1=1,若fn(x)有两个极值点αn、βn,且满足αn+βn=2nαnβn,其中n=1,2….
(1)试用an表示an+1;
(2)求数列{an}的通项公式;
(3)若Tn=α1β1+α2β2+…+αnβn,证明:对一切n∈N*,均有1≤Tn<2.
(1)试用an表示an+1;
(2)求数列{an}的通项公式;
(3)若Tn=α1β1+α2β2+…+αnβn,证明:对一切n∈N*,均有1≤Tn<2.
考点:数列与函数的综合,利用导数研究函数的极值
专题:等差数列与等比数列
分析:(Ⅰ)由fn′(x)=6anx2-6an+1x+6=0,得:anx2-an+1x+1=0,由此利用韦达定理结合已知条件推导出an+1=an+2n,n∈N*.
(Ⅱ)由an+1-an=2n,利用累加法能求出an=2n-1.
(Ⅲ)由αnβn=
>0,得Tn≥T1=1,当n≥2时,αnβn=
<
-
,由此利用裂项求和法能证明对一切n∈N*,均有1≤Tn<2成立.
(Ⅱ)由an+1-an=2n,利用累加法能求出an=2n-1.
(Ⅲ)由αnβn=
| 1 |
| αn |
| 1 |
| an |
| 1 |
| 2n-1-1 |
| 1 |
| 2n-1 |
解答:
(Ⅰ)解:∵函数fn(x)=2anx3-3an+1x2+6x+1,
∴fn′(x)=6anx2-6an+1x+6,
由fn'(x)=0,得:anx2-an+1x+1=0,
∴x=αn、x=βn是上方程的两根,由韦达定理:
,
由已知αn+βn-1=2nαnβn,n∈N*,
∴
-1=
,即an+1=an+2n,n∈N*.…(3分)
(Ⅱ)解:由(Ⅰ)知:an+1-an=2n,n∈N*,
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=2n-1+2n-2+…+2+1
=
=2n-1.…(7分)
(Ⅲ)证明:∵αnβn=
>0,∴Tn≥T1=1,
当n≥2时,αnβn=
=
=
<
=
-
,
Tn=α1β1+α2β2+…+αnβn
<1+(1-
)+…+(
-
)
=2-
<2,
综上,对一切n∈N*,均有1≤Tn<2成立.…(13分)
∴fn′(x)=6anx2-6an+1x+6,
由fn'(x)=0,得:anx2-an+1x+1=0,
∴x=αn、x=βn是上方程的两根,由韦达定理:
|
由已知αn+βn-1=2nαnβn,n∈N*,
∴
| an+1 |
| an |
| 2n |
| an |
(Ⅱ)解:由(Ⅰ)知:an+1-an=2n,n∈N*,
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=2n-1+2n-2+…+2+1
=
| 1-2n |
| 1-2 |
(Ⅲ)证明:∵αnβn=
| 1 |
| αn |
当n≥2时,αnβn=
| 1 |
| an |
| 1 |
| 2n-1 |
| 2n-1-1 |
| (2n-1)(2n-1-1) |
<
| 2n-1 |
| (2n-1)(2n-1-1) |
| 1 |
| 2n-1-1 |
| 1 |
| 2n-1 |
Tn=α1β1+α2β2+…+αnβn
<1+(1-
| 1 |
| 3 |
| 1 |
| 2n-1-1 |
| 1 |
| 2n-1 |
=2-
| 1 |
| 2n-1 |
综上,对一切n∈N*,均有1≤Tn<2成立.…(13分)
点评:本题考查数列的通项公式的求法,考查不等式的证明,是中档题,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
命题:“若x=1,则x2=1”的逆否命题是( )
| A、若x≠1,则x2≠1 |
| B、若x2=1,则x=1 |
| C、若x2≠1,则x≠1 |
| D、若x2≠1,则x=1 |
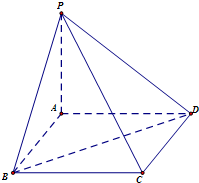 如图,已知ABCD是正方形;P是平面ABCD外一点,且PA⊥面ABCD,PA=AB=3.求:
如图,已知ABCD是正方形;P是平面ABCD外一点,且PA⊥面ABCD,PA=AB=3.求: 如图,在Rt△AOB中,∠OAB=
如图,在Rt△AOB中,∠OAB=