题目内容
求证：f（x）=x2+1在（1，+∞）上是增函数．
考点：函数单调性的性质
专题：函数的性质及应用
分析：根据函数单调性的定义即可得到结论．
解答：
解：证明：设任意的x1，x2∈（1，+∞），且x1＜x2，则
f（x1）-f（x2）=x12+1-x22-1=x12-x22
=（x1-x2）（x1+x2），
∵x1，x2∈（1，+∞），且x1＜x2，
∴x1-x2＜0，x1+x2＞0，
∴f（x1）-f（x2）＜0，
即f（x1）＜f（x2），
∴函数f（x）=x2+1在（1，+∞）上是增函数．
f（x1）-f（x2）=x12+1-x22-1=x12-x22
=（x1-x2）（x1+x2），
∵x1，x2∈（1，+∞），且x1＜x2，
∴x1-x2＜0，x1+x2＞0，
∴f（x1）-f（x2）＜0，
即f（x1）＜f（x2），
∴函数f（x）=x2+1在（1，+∞）上是增函数．
点评：本题主要考查函数单调性的判断，由增函数的定义证明即可，属于基础题．
练习册系列答案
相关题目
设x，y∈R，向量
=（x，-1），
=（1，y），
（4，-2），且
∥
，
⊥
，则|
-
|=（
| a |
| b |
| c |
| a |
| c |
| b |
| c |
| a |
| b |
A、
| ||
B、
| ||
C、2
| ||
| D、10 |
某学校高一年级有20个班，每个班有50名同学，每个班的学号都是从1到50进行编号，现抽调每个班学号为10的同学参加太空授课活动，这种抽样方法是（ ）
| A、分层抽样 | B、抽签抽样 |
| C、随机抽样 | D、系统抽样 |
下列说法正确的有（ ）
①单位向量都相等；②长度相等且方向相反的两个向量一定是共线向量；③若
，
满足|
|＞|
|且
与
同向，则
＞
；④若
=
，则|
|=|
|，反之也成立； ⑤对于任意向量
、
，必有|
+
|≤|
|+|
|．
①单位向量都相等；②长度相等且方向相反的两个向量一定是共线向量；③若
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、①②③ | B、①②④ |
| C、③④⑤ | D、②⑤ |
下列命题中，真命题是（ ）
| A、?x0∈R，e x0≤0 | ||
| B、?x∈R，3x＞x3 | ||
C、“a-b=0”的充分不必要条件是“
| ||
| D、“x＞a2+b2”是“x＞2ab”的必要不充分条件 |
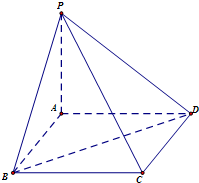如图，已知ABCD是正方形；P是平面ABCD外一点，且PA⊥面ABCD，PA=AB=3．求：