题目内容
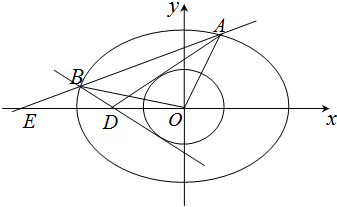 如图,过点D(-2,0)作圆O:x2+y2=r2(0<r<
如图,过点D(-2,0)作圆O:x2+y2=r2(0<r<| 3 |
| x2 |
| 6 |
| y2 |
| 3 |
(Ⅰ)若△OAD的面积为1,求r的值;
(Ⅱ)求证:直线BD与圆O相切.
考点:圆与圆锥曲线的综合
专题:计算题,证明题,直线与圆,圆锥曲线的定义、性质与方程
分析:(Ⅰ)由△OAD的面积为1,运用面积公式,得到yA=1,求得A的坐标,得到AD的方程,由直线和圆相切的条件,即可得到半径r;
(Ⅱ)设直线AE:y=k(x+3),联立椭圆方程C:
+
=1,消去y,得到关于x的二次方程,设A(x1,y1),B(x2,y2),则y1=k(x1+3),y2=k(x2+3),运用韦达定理,设A关于x轴的对称点为A'(x1,-y1),由斜率公式,求出直线BD,A'D的斜率,作差注意化简变形,证明它们相等即可.
(Ⅱ)设直线AE:y=k(x+3),联立椭圆方程C:
| x2 |
| 6 |
| y2 |
| 3 |
解答:
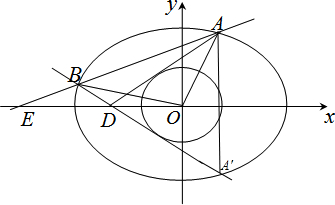 (Ⅰ)解:∵△OAD的面积为1,设yA>0,
(Ⅰ)解:∵△OAD的面积为1,设yA>0,
∴
×2•yA=1,即yA=1,A(2,1),
∴直线AD:y=
(x+2),
∴由直线AD与圆相切,得到
d=r=
=
.
(Ⅱ)证明:设直线AE:y=k(x+3),联立椭圆方程C:
+
=1,消去y,
得(1+2k2)x2+12k2x+(18k2-6)=0,
设A(x1,y1),B(x2,y2),则y1=k(x1+3),y2=k(x2+3),
则x1+x2=-
,x1x2=
,
设A关于x轴的对称点为A'(x1,-y1),
则kBD=
,kA'D=
,
则kBD-kA'D=
-
=
+
=k(2+
+
)
=k(2+
)=k(2+
)=k(2-2)=0.
∴kBD=kA'D,即B,D,A'共线,
故由AD和圆相切,得直线BD和圆也相切.
 (Ⅰ)解:∵△OAD的面积为1,设yA>0,
(Ⅰ)解:∵△OAD的面积为1,设yA>0,∴
| 1 |
| 2 |
∴直线AD:y=
| 1 |
| 4 |
∴由直线AD与圆相切,得到
d=r=
| |2| | ||
|
2
| ||
| 17 |
(Ⅱ)证明:设直线AE:y=k(x+3),联立椭圆方程C:
| x2 |
| 6 |
| y2 |
| 3 |
得(1+2k2)x2+12k2x+(18k2-6)=0,
设A(x1,y1),B(x2,y2),则y1=k(x1+3),y2=k(x2+3),
则x1+x2=-
| 12k2 |
| 1+2k2 |
| 18k2-6 |
| 1+2k2 |
设A关于x轴的对称点为A'(x1,-y1),
则kBD=
| y2 |
| x2+2 |
| -y1 |
| x1+2 |
则kBD-kA'D=
| y2 |
| x2+2 |
| -y1 |
| x1+2 |
| k(x2+3) |
| x2+1 |
| k(x1+3) |
| x1+2 |
| 1 |
| x1+2 |
| 1 |
| x2+2 |
=k(2+
| x1+x2+4 |
| x1x2+4+2x1+2x2 |
| -12k2+4+8k2 |
| 4+8k2+18k2-6-24k2 |
∴kBD=kA'D,即B,D,A'共线,
故由AD和圆相切,得直线BD和圆也相切.
点评:本题考查直线与圆的位置关系:相切,以及直线的斜率和方程有关知识,考查直线方程和椭圆方程联立,消去一个未知数,运用韦达定理,考查化简推理和运算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
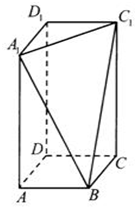 在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1,C1,B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,这个几何体的体积为
在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1,C1,B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,这个几何体的体积为 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD.求证:平面PDC⊥平面PAD.
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD.求证:平面PDC⊥平面PAD.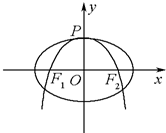 如图,抛物线C:y=-
如图,抛物线C:y=-