题目内容
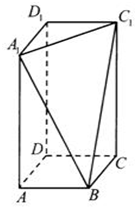 在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1,C1,B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,这个几何体的体积为
在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1,C1,B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,这个几何体的体积为| 40 |
| 3 |
(1)证明:直线A1B∥平面CDD1C1;
(2)求棱A1A的长;
(3)在线段BC1上是否存在点P,使直线A1P与C1D垂直,如果存在,求线段A1P的长,如果不存在,请说明理由.
考点:直线与平面平行的判定,点、线、面间的距离计算
专题:空间位置关系与距离
分析:(1)根据长方体的性质推断出平面A1AB∥平面CDD1C1.进而根据线面平行的判定定理推断出A1B∥平面CDD1C1.
(2)设A1A=h,进而根据几何体的体积关系求得棱柱ABCD-A1B1C1D1的体积,进而利用体积公式求得h.
(3)在平面CC1D1D中作D1Q⊥C1D交CC1于Q,过Q作QP∥CB交BC1于点P,根据线面垂直的性质推断出A1D1⊥平面CC1D1D,进而根据QP∥CB,CB∥A1D1,推断出QP∥A1D1,利用线面垂直的性质证明出A1P⊥C1D.通过△D1C1Q∽Rt△C1CD,利用比例关系求得C1Q,最后利用平方关系求得A1P.
(2)设A1A=h,进而根据几何体的体积关系求得棱柱ABCD-A1B1C1D1的体积,进而利用体积公式求得h.
(3)在平面CC1D1D中作D1Q⊥C1D交CC1于Q,过Q作QP∥CB交BC1于点P,根据线面垂直的性质推断出A1D1⊥平面CC1D1D,进而根据QP∥CB,CB∥A1D1,推断出QP∥A1D1,利用线面垂直的性质证明出A1P⊥C1D.通过△D1C1Q∽Rt△C1CD,利用比例关系求得C1Q,最后利用平方关系求得A1P.
解答:
(1)证明:∵ABCD-A1B1C1D1是长方体,
∴平面A1AB∥平面CDD1C1.
∵A1B?平面A1AB,A1B?平面CDD1C1,
∴A1B∥平面CDD1C1.
(2)解:设A1A=h,
∵几何体ABCD-A1C1D1的体积为
,
∴VABCD-A1C1D1=VABCD-A1B1C1D1-VB-A1B1C1=
,
即SABCD×h-
×S△A1B1C1×h=
,
即2×2×h-
×
×2×2×h=
,解得h=4.
∴A1A的长为4.
(3)在平面CC1D1D中作D1Q⊥C1D交CC1于Q,过Q作QP∥CB交BC1于点P,则A1P⊥C1D.
∵A1D1⊥平面CC1D1D,C1D?平面CC1D1D,
∴C1D⊥A1D1,而QP∥CB,CB∥A1D1,
∴QP∥A1D1,
又∵A1D1∩D1Q=D1,
∴C1D⊥平面A1PQC1,
且A1P?平面A1PQC1,
∴A1P⊥C1D.
∵△D1C1Q∽Rt△C1CD,
∴
=
,
∴C1Q=1,
又∵PQ∥BC,
∴PQ=
BC=
.
∵四边形A1PQD1为直角梯形,且高D1Q=
,
∴A1P=
=
.
∴平面A1AB∥平面CDD1C1.
∵A1B?平面A1AB,A1B?平面CDD1C1,
∴A1B∥平面CDD1C1.
(2)解:设A1A=h,
∵几何体ABCD-A1C1D1的体积为
| 40 |
| 3 |
∴VABCD-A1C1D1=VABCD-A1B1C1D1-VB-A1B1C1=
| 40 |
| 3 |
即SABCD×h-
| 1 |
| 3 |
| 40 |
| 3 |
即2×2×h-
| 1 |
| 3 |
| 1 |
| 2 |
| 40 |
| 3 |
∴A1A的长为4.
(3)在平面CC1D1D中作D1Q⊥C1D交CC1于Q,过Q作QP∥CB交BC1于点P,则A1P⊥C1D.
∵A1D1⊥平面CC1D1D,C1D?平面CC1D1D,
∴C1D⊥A1D1,而QP∥CB,CB∥A1D1,
∴QP∥A1D1,
又∵A1D1∩D1Q=D1,
∴C1D⊥平面A1PQC1,
且A1P?平面A1PQC1,
∴A1P⊥C1D.
∵△D1C1Q∽Rt△C1CD,
∴
| C1Q |
| CD |
| D1C1 |
| C1C |
∴C1Q=1,
又∵PQ∥BC,
∴PQ=
| 1 |
| 4 |
| 1 |
| 2 |
∵四边形A1PQD1为直角梯形,且高D1Q=
| 5 |
∴A1P=
(2-
|
| ||
| 2 |
点评:本题主要考查了线面平行和线面垂直的判定定理的运用.考查了学生推理和分析能力.

练习册系列答案
相关题目
已知双曲线C:
-
=1(a>0,b>0)的离心率为
,且过点(
,-2),则C的实轴长为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 3 |
| A、2 | ||
| B、2 | ||
C、
| ||
D、2
|
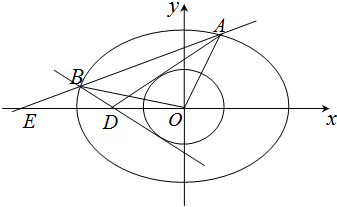 如图,过点D(-2,0)作圆O:x2+y2=r2(0<r<
如图,过点D(-2,0)作圆O:x2+y2=r2(0<r<