题目内容
某学校课题组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级12名学生某次考试成绩如下表所示:
若单科成绩85分以上(含85分),则该科成绩为优秀.
(1)根据上表完成下面的2×2列联表(单位:人):
(2)根据题(1)中表格的数据计算,有多大的把握,认为学生的数学成绩与物理成绩之间有关系?(小数点后三位有效)
友情提示:随机变量K2=
;
独立检验随机变量K2的临界值参考表:
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 数学成绩 | 95 | 85 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 83 | 75 |
| 物理成绩 | 90 | 83 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 86 | 63 |
(1)根据上表完成下面的2×2列联表(单位:人):
| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 物理成绩优秀 | |||
| 物理成绩不优秀 | |||
| 合计 |
友情提示:随机变量K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
独立检验随机变量K2的临界值参考表:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
考点:独立性检验的应用
专题:应用题,概率与统计
分析:(1)根据科成绩在85分以上(含85分),则该科成绩为优秀,结合表格中的数据,即可得2×2列联表;
(2)利用列联表中的数据,利用公式,再与提供的临界值比较,即可得结论.
(2)利用列联表中的数据,利用公式,再与提供的临界值比较,即可得结论.
解答:
解:(1)根据上表完成下面的2×2列联表(单位:人):
(2)K2=
=3.6>3.841,
所以,我们有95%的把握认为:学生的数学成绩与物理成绩之间有关系
| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 物理成绩优秀 | 4 | 1 | 5 |
| 物理成绩不优秀 | 1 | 4 | 5 |
| 合计 | 5 | 5 | 10 |
| 10×(16-1)2 |
| 5×5×5×5 |
所以,我们有95%的把握认为:学生的数学成绩与物理成绩之间有关系
点评:本题以实际问题为载体,考查独立性检验的应用,考查列联表及K2的计算,属于基础题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
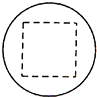 已知某一多面体内接于球构成一个简单组合体,如果该组合体的正视图、侧视图、俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是( )
已知某一多面体内接于球构成一个简单组合体,如果该组合体的正视图、侧视图、俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是( )| A、64π | B、32π |
| C、16π | D、12π |
已知双曲线C:
-
=1(a>0,b>0)的离心率为
,且过点(
,-2),则C的实轴长为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 3 |
| A、2 | ||
| B、2 | ||
C、
| ||
D、2
|

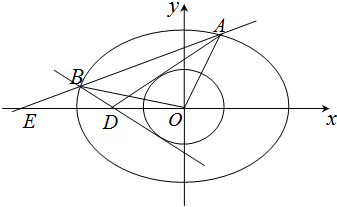 如图,过点D(-2,0)作圆O:x2+y2=r2(0<r<
如图,过点D(-2,0)作圆O:x2+y2=r2(0<r<