题目内容
牛奶保鲜时间因储藏时温度的不同而不同,假定保鲜时间与储藏温度间的关系为指数型函数,若牛奶放在0℃的冰箱中,保鲜时间约是192h,而在22℃的厨房中则约是42h
(1)写出保鲜时间y(单位:h)关于储藏温度x(单位:℃)的函数解析式
(2)利用(1)中结论,指出温度在30℃和16℃的保鲜时间(精确到1h)
(3)运用上面的数据,作此函数的图象.
(1)写出保鲜时间y(单位:h)关于储藏温度x(单位:℃)的函数解析式
(2)利用(1)中结论,指出温度在30℃和16℃的保鲜时间(精确到1h)
(3)运用上面的数据,作此函数的图象.
考点:指数函数的实际应用
专题:函数的性质及应用
分析:(1)设y=k•ax(k≠0,a>0且a≠1),则利用牛奶放在0℃的冰箱中,保鲜时间约为192h,放在22℃的厨房中,保鲜时间约为42h,即可得出函数解析式;
(2)x=30°时,y=192•(
)
,x=16°时,y=192•(
)
,运用解析式求解即可
(3)判断单调性根据解析式.
(2)x=30°时,y=192•(
| 7 |
| 32 |
| 15 |
| 11 |
| 7 |
| 32 |
| 1 |
| 2 |
(3)判断单调性根据解析式.
解答:
解:(1)设y=k•ax(k≠0,a>0且a≠1),则有
,
∴
,
∴y=192•(
)
.x≥0.
(2)x=30°时,y=192•(
)
,
x=16°时,y=192•(
)
,
(3)运用函数解析式y=192•(
)
.x≥0.
单调递减函数.
|
∴
|
∴y=192•(
| 7 |
| 32 |
| x |
| 22 |
(2)x=30°时,y=192•(
| 7 |
| 32 |
| 15 |
| 11 |
x=16°时,y=192•(
| 7 |
| 32 |
| 1 |
| 2 |
(3)运用函数解析式y=192•(
| 7 |
| 32 |
| x |
| 22 |
单调递减函数.
点评:本题考查了指数函数的性质,运用方程组的方法求解,计算较麻烦.

练习册系列答案
相关题目
(2-
)8展开式中各项系数的和为( )
| x |
| A、-1 | B、1 |
| C、256 | D、-256 |
设命题p:若|
|=|
|=
,且
与
的夹角是
,则向量
在
方向上的投影是1;命题q:“x≥1”是“
≤1”的充分不必要条件,下列判断正确的是( )
| a |
| b |
| 2 |
| a |
| b |
| 3π |
| 4 |
| b |
| a |
| 1 |
| x |
| A、p∨q是假命题 |
| B、p∧q是真命题 |
| C、p∨q是真命题 |
| D、﹁q为真命题 |
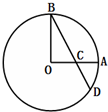 如图,A,B是圆O上两点,且OA⊥OB,OA=1,C为OA的中点,连接BC并延长交圆O于点D,则CD=
如图,A,B是圆O上两点,且OA⊥OB,OA=1,C为OA的中点,连接BC并延长交圆O于点D,则CD=