题目内容
设命题p:若|
|=|
|=
,且
与
的夹角是
,则向量
在
方向上的投影是1;命题q:“x≥1”是“
≤1”的充分不必要条件,下列判断正确的是( )
| a |
| b |
| 2 |
| a |
| b |
| 3π |
| 4 |
| b |
| a |
| 1 |
| x |
| A、p∨q是假命题 |
| B、p∧q是真命题 |
| C、p∨q是真命题 |
| D、﹁q为真命题 |
考点:复合命题的真假
专题:简易逻辑
分析:首先利用向量的数量积判断出命题p是真命题,进一步判断出命题q是假命题,最后判断出结论.
解答:
解:命题p:若|
|=|
|=
,且
与
的夹角是
,则向量
在
方向上的投影是|
|cos
=-1.
所以:命题P是假命题.
命题q:“x≥1”可以得到:“
≤1”,
但
≤1的解集是:{x|x≥1或x<0}
所以:“x≥1”是“
≤1”的充分不必要条件.
所以:命题q是真命题.
所以p∨q是真命题.
故选:C.
| a |
| b |
| 2 |
| a |
| b |
| 3π |
| 4 |
| b |
| a |
| b |
| 3π |
| 4 |
所以:命题P是假命题.
命题q:“x≥1”可以得到:“
| 1 |
| x |
但
| 1 |
| x |
所以:“x≥1”是“
| 1 |
| x |
所以:命题q是真命题.
所以p∨q是真命题.
故选:C.
点评:本题考查的知识要点:向量的数量积的应用,四种命题的应用,简易逻辑中且是命题和或是命题的应用.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
实数x、y满足x2+2xy+y2+4x2y2=4,则x-y的最大值为( )
A、
| ||
B、
| ||
C、
| ||
D、2
|
数列{an}是公差d不为零的等差数列,其前n项和为Sn,若记数据a1,a2,a3,…,a2015的方差为λ1,数据
,
,
,…,
的方差为λ2,则( )
| S1 |
| 1 |
| S2 |
| 2 |
| S3 |
| 3 |
| S2015 |
| 2015 |
| A、λ1>λ2 |
| B、λ1=λ2 |
| C、λ1<λ2 |
| D、与的大小关系与公差的正负有关 |
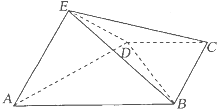 如图,在四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,AB=4,BC=CD=EA=ED=2,F是线段EB的中点.
如图,在四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,AB=4,BC=CD=EA=ED=2,F是线段EB的中点.