题目内容
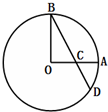如图，A，B是圆O上两点，且OA⊥OB，OA=1，C为OA的中点，连接BC并延长交圆O于点D，则CD=考点：与圆有关的比例线段
专题：推理和证明
分析：由已知得OB=1，OC=
，BC=
=
，延长AO，交圆O于点E，由相交弦定理得：AC•CE=BC•CD，由此能求出CD．
| 1 |
| 2 |
1+
|
| ||
| 2 |
解答：
解：∵A，B是圆O上两点，且OA⊥OB，OA=1，C为OA的中点，
∴OB=1，OC=
，BC=
=
，
延长AO，交圆O于点E，
由相交弦定理得：AC•CE=BC•CD，
∴CD=
=
=
．
故答案为：
．
∴OB=1，OC=
| 1 |
| 2 |
1+
|
| ||
| 2 |
延长AO，交圆O于点E，
由相交弦定理得：AC•CE=BC•CD，
∴CD=
| AC×CE |
| BC |
| ||||
|
3
| ||
| 10 |
故答案为：
3
| ||
| 10 |
点评：本题考查与圆有关的线段长的求法，是中档题，解题时要注意圆的性质和相交弦定理的合理运用．
练习册系列答案
相关题目
如图，圆内接四边形ABCD的边BC与AD的延长线交于点E，点F在BA的延长线上．设l、m是两条不同的直线，α，β是两个不同的平面，则下列命题为真命题的是（ ）
| A、若m∥l，m∥α，则l∥α |
| B、若m⊥α，l⊥m，则l∥α |
| C、若α∥β，l⊥α，m∥β，则l⊥m |
| D、若m?α，m∥β，l?β，l∥α，则α∥β |
数列{an}是公差d不为零的等差数列，其前n项和为Sn，若记数据a1，a2，a3，…，a2015的方差为λ1，数据
，
，
，…，
的方差为λ2，则（ ）
| S1 |
| 1 |
| S2 |
| 2 |
| S3 |
| 3 |
| S2015 |
| 2015 |
| A、λ1＞λ2 |
| B、λ1=λ2 |
| C、λ1＜λ2 |
| D、与的大小关系与公差的正负有关 |