题目内容
7.要得到函数y=cos(2x-$\frac{π}{6}$)的图象,只需将函数y=sin2x的图象( )| A. | 向左平移$\frac{π}{12}$个单位 | B. | 向左平移$\frac{π}{6}$个单位 | ||
| C. | 向右平移$\frac{π}{12}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
分析 先根据诱导公式将函数化简,再根据左加右减的原则进行平移从而可得到答案.
解答 解:∵y=cos(2x-$\frac{π}{6}$)=cos($\frac{π}{6}$-2x)=sin(2x+$\frac{π}{3}$)=sin[2(x+$\frac{π}{6}$)],
∴将函数y=sin2x的图象向左平移$\frac{π}{6}$个单位即可得到函数y=cos(2x-$\frac{π}{6}$)的图象.
故选:B.
点评 本题主要考查诱导公式的应用和三角函数的平移,三角函数平移时一定要遵循左加右减上加下减的原则.

练习册系列答案
相关题目
17.袋子中装有形状和大小完全相同的五个小球,每个小球上分别标有“1”“2”“3”“4”“6”这五个数,现从中随机选取三个小球,则所选的三个小球上的数恰好能构成一个等差数列的概率是( )
| A. | $\frac{3}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{10}$ | D. | $\frac{1}{20}$ |
19.已知数列{an}为等差数列,若a2+a6+a10=$\frac{π}{2}$,则tan(a3+a9)的值为( )
| A. | 0 | B. | $\frac{\sqrt{3}}{3}$ | C. | 1 | D. | $\sqrt{3}$ |
16.点B是点A(1,2,3)在坐标平面yOz内的射影,则|OB|等于( )
| A. | $\sqrt{14}$ | B. | $\sqrt{13}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{10}$ |
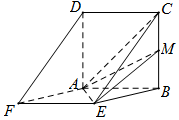 已知边长为2的正方形ABCD与菱形ABEF所在平面互相垂直,M为BC中点.
已知边长为2的正方形ABCD与菱形ABEF所在平面互相垂直,M为BC中点.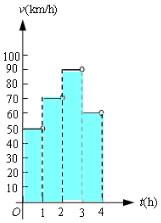 一辆汽车在某段路程中的行驶速率与时间的关系如图所示.
一辆汽车在某段路程中的行驶速率与时间的关系如图所示.