题目内容
2．已知函数f（x）=x|x-2|（Ⅰ）写出不等式f（x）＞0的解集；
（Ⅱ）解不等式f（x）＜x．
分析 （Ⅰ）根据|x-2|≥0，求出不等式的解集即可；（Ⅱ）通过讨论x的范围，得到关于x的不等式组，解出即可．
解答 解：（Ⅰ）∵|x-2|≥0，
故f（x）＞0的解集是：{x|x＞0且x≠2}；
（Ⅱ）由x|x-2|＜x，
得：$\left\{\begin{array}{l}{x＞0}\\{|x-2|＜1}\end{array}\right.$，或$\left\{\begin{array}{l}{x＜0}\\{|x-2|＞1}\end{array}\right.$，
解得：1＜x＜3，或x＜0，
故不等式的解集是{x|1＜x＜3或x＜0}．
点评 本题考查了解绝对值不等式问题，考查分类讨论思想，是一道基础题．
练习册系列答案
相关题目
7．要得到函数y=cos（2x-$\frac{π}{6}$）的图象，只需将函数y=sin2x的图象（ ）
| A． | 向左平移$\frac{π}{12}$个单位 | B． | 向左平移$\frac{π}{6}$个单位 | ||
| C． | 向右平移$\frac{π}{12}$个单位 | D． | 向右平移$\frac{π}{6}$个单位 |
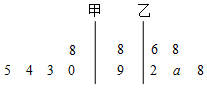如图是甲、乙两位同学高二上学期历史成绩的茎叶图，有一个数字被污损，用a（3≤a≤8且a∈N）表示．