题目内容
16.点B是点A(1,2,3)在坐标平面yOz内的射影,则|OB|等于( )| A. | $\sqrt{14}$ | B. | $\sqrt{13}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{10}$ |
分析 根据点B是点A(1,2,3)在yOz坐标平面内的射影,O为坐标原点,得到点B的坐标,根据两点之间的距离公式得到结果.
解答 解:∵点B是点A(1,2,3)在yOz坐标平面内的射影
∴B点的坐标是(0,2,3)
∴|OB|等于$\sqrt{13}$,
故选B.
点评 本题考查空间直角坐标系,考查空间中两点间的距离公式,是一个基础题,解题的关键是,一个点在一个坐标平面上的射影的坐标同这个点的坐标的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.齐王与田忌赛马,每场比赛三匹马各出场一次,共赛三次,以胜的次数多者为赢.田忌的上马优于齐王的中马,劣于齐王的上马,田忌的中马优于齐王的下马,劣于齐王的中马,田忌的下马劣于齐王的下马.现各出上、中、下三匹马分组进行比赛,如双方均不知对方马的出场顺序,则田忌获胜的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{2}$ |
7.要得到函数y=cos(2x-$\frac{π}{6}$)的图象,只需将函数y=sin2x的图象( )
| A. | 向左平移$\frac{π}{12}$个单位 | B. | 向左平移$\frac{π}{6}$个单位 | ||
| C. | 向右平移$\frac{π}{12}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
10.若存在x0>1,使不等式(x0+1)ln x0<a(x0-1)成立,则实数a的取值范围是 ( )
| A. | (-∞,2) | B. | (2,+∞) | C. | (1,+∞) | D. | (4,+∞) |
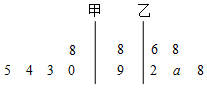 如图是甲、乙两位同学高二上学期历史成绩的茎叶图,有一个数字被污损,用a(3≤a≤8且a∈N)表示.
如图是甲、乙两位同学高二上学期历史成绩的茎叶图,有一个数字被污损,用a(3≤a≤8且a∈N)表示.