题目内容
12.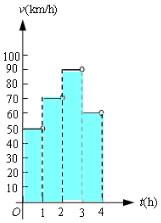 一辆汽车在某段路程中的行驶速率与时间的关系如图所示.
一辆汽车在某段路程中的行驶速率与时间的关系如图所示.(1)求图中阴影部分的面积,并说明所求面积的实际含义;
(2)假设这辆汽车在行驶该段路程前里程表的读数是8018km,试求汽车在行驶这段路程时里程表读数s(km)与时间t (h)的函数解析式,并作出相应的图象.
分析 (1)由频率分布图能求出阴影部分的面积,表示汽车在4小时内行驶的路程.
(2)由这辆汽车在行驶该段路程前里程表的读数是8018km,结合频率分布直方图能求出汽车在行驶这段路程时里程表读数s(km)与时间t (h)的函数解析式,并能作出图象.
解答 解:(1)阴影部分的面积为:
50+70+90+60=270,
表示汽车在4小时内行驶的路程为270 km. (4分)
(2)∵这辆汽车在行驶该段路程前里程表的读数是8018km,
汽车在行驶这段路程时里程表读数s(km)与时间t (h)的函数解析式为:
$s=\left\{\begin{array}{l}50t+8018,0≤t<1\\ 70(t-1)+8068,1≤t<2\\ 90(t-2)+8138,2≤t<3\\ 60(t-3)+8228,3≤t≤4.\end{array}\right.$(4分)
图象如下图: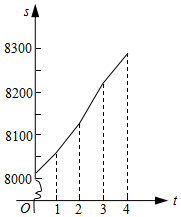
(4分)
点评 本题考查阴影面积的求法,考查函数解析式及图象的求法,是基础题,解题时要认真审题,注意频率分布直方图的性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
2.已知点P(-2$\sqrt{2}$,0)是椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点,过点P作圆O:x2+y2=4的切线,切点为A,B,若直线AB恰好过椭圆C的左焦点F,则a2+b2的值是( )
| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
3.设等比数列{an}的前n项为Sn,若a1=2,$\frac{{S}_{6}}{{S}_{2}}$=21,则数列{$\frac{1}{{a}_{n}}$}的前5项和为( )
| A. | $\frac{1}{2}$或$\frac{11}{32}$ | B. | $\frac{1}{2}$或$\frac{31}{32}$ | C. | $\frac{11}{32}$或$\frac{31}{32}$ | D. | $\frac{11}{32}$或$\frac{5}{2}$ |
7.要得到函数y=cos(2x-$\frac{π}{6}$)的图象,只需将函数y=sin2x的图象( )
| A. | 向左平移$\frac{π}{12}$个单位 | B. | 向左平移$\frac{π}{6}$个单位 | ||
| C. | 向右平移$\frac{π}{12}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
4.存在函数f(x)满足对于任意x∈R都有( )
| A. | f(|x|)=x+1 | B. | f(x2)=2x+1 | C. | f(|x|)=x2+2 | D. | f($\sqrt{x}$)=3x+2 |