题目内容
19.已知数列{an}为等差数列,若a2+a6+a10=$\frac{π}{2}$,则tan(a3+a9)的值为( )| A. | 0 | B. | $\frac{\sqrt{3}}{3}$ | C. | 1 | D. | $\sqrt{3}$ |
分析 由等差数列的性质得${a}_{6}=\frac{π}{6}$.从而a3+a9=2a6=$\frac{π}{3}$,由此能求出tan(a3+a9)的值.
解答 解:∵数列{an}为等差数列,a1+a6+a10=$\frac{π}{2}$,
∴a2+a6+a10=3a6=$\frac{π}{2}$,解得${a}_{6}=\frac{π}{6}$.
∴a3+a9=2a6=$\frac{π}{3}$,
∴tan(a3+a9)=tan$\frac{π}{3}$=$\sqrt{3}$.
故选:D.
点评 本题考查正切值的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
9.直线y=2016与正切曲线y=tan3x相交的相邻两点间的距离是( )
| A. | π | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
7.要得到函数y=cos(2x-$\frac{π}{6}$)的图象,只需将函数y=sin2x的图象( )
| A. | 向左平移$\frac{π}{12}$个单位 | B. | 向左平移$\frac{π}{6}$个单位 | ||
| C. | 向右平移$\frac{π}{12}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
10.若存在x0>1,使不等式(x0+1)ln x0<a(x0-1)成立,则实数a的取值范围是 ( )
| A. | (-∞,2) | B. | (2,+∞) | C. | (1,+∞) | D. | (4,+∞) |
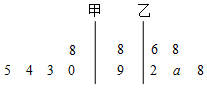 如图是甲、乙两位同学高二上学期历史成绩的茎叶图,有一个数字被污损,用a(3≤a≤8且a∈N)表示.
如图是甲、乙两位同学高二上学期历史成绩的茎叶图,有一个数字被污损,用a(3≤a≤8且a∈N)表示.